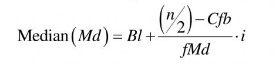DAFTAR ISI
TINJAUAN MATA KULIAH
MODUL 1 : KONSEP DASAR STATISTIKA
MODUL 2 : PENYAJIAN DATA
MODUL 3 : UKURAN PEMUSATAN DAN UKURAN PENYEBARAN
MODUL 4 : PROBABILITA
MODUL 5 : PENARIKAN SAMPEL
MODUL 6 : ESTIMASI DAN UJI HIPOTESIS
MODUL 7 : PENGUJIAN HIPOTESIS SATU SAMPEL
MODUL 8 : PENGUJIAN HIPOTESIS DUA SAMPEL
MODUL 9 : PENGUJIAN HIPOTESIS LEBIH DARI DUA SAMPEL DAN DUA RATA-RATA POPULASI.
TINJAUAN MATA KULIAH
Pengantar Statistik Sosial merupakan mata kuliah yang mempelajari dasar-dasar statistik dalam ilmu sosial. Mata kuliah ini bermanfaat karena akan memberikan bekal dasar untuk memahami mata kuliah lainnya, seperti mata kuliah metode penelitian sosial.
Setelah mempelajari mata kuliah ini, diharapkan mampu menerapkan statistika deskriptif dan inferensia. Secara khusus anda diharapkan mampu :
1. menerapkan konsep-konsep dasar statistika
2. menerapkan penyajian data
3. menerapkan ukuran pemusatan dan ukuran penyebaran
4. menghitung probabilita
5. menerapkan metode penarikan sampel
6. melakukan estimasi dan uji hipotesis
MODUL 1 :
KONSEP DASAR STATISTIKA
Apakah anda penggemar Piala Dunia? Jika ya, pernakah anda mencoba untuk menerka siapakah yang akan menjadi juara dunia, pada saat penyelenggaraan piala dunia?. Pada saat anda mencoba untuk menerka, tentunya anda akan mencoba mencari tahu bagaimana kelemahan dan kelebihan dari setiap tim yang akan berlaga, dan tentunya anda membutuhkan bermacam informasi. Setelah anda memiliki bermacam informasi, mulailah anda berhitung sehingga anda sampai pada kesimpulan bahwa Tim A akan memenangkan seluruh pertandingan dan menjadi juara . Proses ini pada dasarnya merupakan salah satu gambaran tetang statistika.
Apa sebenarnya statistika? Apakah sama dengan Statistik? Mengapa kita harus mempelajari Statistik? Pada Modul 1 ini akan mempelajari tentang berbagai konsep dasar yang ada di dalam statistik. Mengetahui apa saja kegunaan mempelajari statistika, dan dasar yang harus dikenali sebelum mempelajri materi lebih lanjut.
Untuk bisa memahami statistika, dibutuhkan banyak praktik yang dapat dilakukan dengan mencoba mengerjakan berbagai latihan yang ada, dan juga mencoba mengerjakan berbagai latihan yang ada. Setelah mempelajari modul 1 ini diharapkan dapat memahami :
1. Pengertian Statistika
2. Manfaat mempelajari statistika
3. Klasifikasi statistika
4. Skala Pengukuran.
KEGIATAN BELAJAR 1 :
PENGERTIAN DAN KLASIFIKASI STATISTIKA
A. PENGERTIAN STATISTIKA
Apakah anda pernah mendengar kata Statistika? Mungkin anda akan menjawab "kalau statistik, ya, saya sering mendengar". Lalu, apakah ada perbedaan antara statistik dan statistika? Kita akan mencoba mencari tahu apa perbedaan antara statistik dan statistika.
Kita akan mulai dari konsep yang lebih sering didengar yaitu kata statistik. seperti telah disampaikan anda sering mendengar, melihat, dan bahkan memanfaatkan berbagai informasi yang ada di sekitar kita. Kita mungkin pernah menggunakan informasi tentang berbagai kebijakan politik yang dibuat oleh partai politik sehingga kita bisa memutuskan apakah kita akan memilih partai politik tersebut atau partai politik yang lain.
Atau kita pernah mendengar tenrtang kemungkinan pemerintah menaikkan pajak kendaraan sehingga kita bisa mengantisipasi, apakah akan membeli kendaraan atau tidak. Nah, berbagai informasi itulah sesungguhnya yang dimaksudkan dengan statistik. Dengan demikian, kita bisa juga mengatakan bahwa statistik adalah suatu kumpulan yang tersusun lebih dari satu angka.
Kita coba lihat beberapa contoh statistik :
1. Lingkar Survei Indonesia (LSI) mendapati hampir 54 persen responden tidak puas dengan pemerintahan Joko Widodo (Jokowi), sedangkan 42 persen menyatakan puas. Survei melalui ponsel itu, dilakukan terhadap 1.200 orang di 34 provinsi pada 26 dan 27 Januari lalu.
2. Pada tahun 2008, misalnya jumlah mahasiswa berusia 18-24 tahun di universitas berstatus negeri ini baru 2.200 orang per semester. Namun, pada tahun 2011 jumlah mahasiswa baru usia 18-24 tahun hampir 12.500 orang.
3. "Jumlah penduduk Indonesia tahun 2012 sekitar 230 juta jiwa. Untuk mengetahui pengaruh pertumbuhan penduduk bukan hanya berdasarkan faktor jumlah, tetapi juga struktur dan persebaran,"Jelas Sudibyo. Struktur ini dipengaruhi oleh Triple Burden, yaitu jumlah usia sekolah dan balita sebesar 28,87 %, angkatan kerja 63,54 %, dan lansia mencpai 7,59 %. Sudibyo menilai kalau jumlah ini akan terus meningkat terutama lansia yang saat ini sudah menembus angka 17 juta jiwa.
Jika pengertian statistik lebih mengarah kepada informasi, pengertian statistika mengarah ke pengertian yang lebih luas. Statistika adalah suatu metode yang digunakan dalam pengumpulan dan analisis data sehingga dapat diperoleh informasi yang berguna.
Pada dasarnya statistika menyediakan prinsip dan metodologi untuk merancang proses pengumpulan data, meringkas data, menyajikan data, serta melakukan interprestasi data, analisis data, serta mengambil kesimpulan.
Dengan kata lain, Statistika adalah ilmu yang mengumpulkan, menata, menyajikan, menganalisis, serta menginterprestasikan data angka, dengan tujuan membantu pengambilan keputusan yang efektif. Dengan demikian, didalam statistika terkandung konsep statistik.
Dalam Statistika, kita akan banyak mempelajari tentang berbagai teknik yang bisa digunakan dalam berbagai hal, seperti dalam penyajian data, analisis data, pengelompokkan data, dsb yang akan dipelajari lebih lanjut dalam modul selanjutnya.
1. Alasan Mempelajari Statistika
Perlukah kita mempelajari statistika? Anda tentunya pernah mempertanyakan hal ini, apalagi kita ketahui bersama bahwa saat ini sudah banyak program yang bisa kita gunakan untuk membantu kita dalam menangani statistika. Program Excel yang ada di seluruh komputer, merupakan salah satu program yang banyak membantu kita dalam statistika.
Dalam penelitian sosial, SPSS dan berbagai macam model sejenis, juga sudah banyak digunakan oleh berbagai kalangan dalam statistika. Jadi, kembali ke pertanyaan awal kita, apakah kita masih perlu mempelajari statistika? Jawabannya tentu saja "Ya". Ingat bahwa berbagai program yang ada hanyalah merupakan alat yang bisa kita gunakan untuk mempermudah pekerjaan kita. Namun, seperti juga alat yang lain maka rumus itu, hanya alat yang bisa kita gunakan secara benar maupun secara tidak benar. Sebuah pisau bisa kita gunakan secara benar, dengan memanfaatkan pisau itu untuk memotong buah. namun pisau yang sama bisa kita gunakan secara salah untuk melukai sesama manusia. Dengan demikian, sekalipun kita menggunakan program SPSS, namun jika pemakaiannya salah maka hasilnya juga akan salah, dan pada akhirnya keputusan yang akan kita ambil juga salah.
Kembali pada pertanyaan apakah masih perlu kita mempelajari statistika? Untuk menjawab pertanyaan tersebut, kita perlu memahami terlebih dahulu, bahwa statistika merupakan sebuah alat, yang bisa berguna jika kita gunakan secara benar dan bisa tidak berguna jika kita gunakan secara salah.
Sering kita mendengar adanya manipulasi data yang salah satunya adalah melalui statistika. Kita coba ambil contoh berikut ini; Pemerintah mengklaim bahwa selama pemerintahan berjalan dua tahun, kesejahteraan masyarakat mengalami peningkatan tajam, hal ini berdasarkan data bahwa masyarakat yang berada di garis kemiskinan hanya sejumlah 5% dari seluruh penduduk yang ada.
Apakah ada yang salah dengan klaim pemerintah tersebut? Jika kita tidak memahami statistika, kita tentunya akan percaya saja pada klaim pemerintah, apalagi data yang menunjukkan bahwa masyarakat yang berada di garis kemiskinan memang menunjukkan data yang demikian.
Namun demikian, jika kita memahami tentang statistika, kita tidak akan percaya. Kita perlu melihat lebih jauh sehingga kita akan melihat bahwa ada data yang disembunyikan dalam laporan tersebut. Jika data yang berada pada garis kemiskinan hanya 5% dan data itu benar, namun demikian ternyata data lain menunjukkan bahwa 35% penduduk yang justru berada di bawah garis kemiskinan. Klaim pemerintah tidak salah, namun ada manipulasi dengan tidak menampilkan data tentang penduduk yang berada di bawah garis kemiskinan. Nah kondisi inilah yang menunjukkan bahwa kita tetap harus mempelajari statistika.
Contoh lain, mengenai pentingnya mempelajari statistika adalah berikut ini. Anda adalah seorang pimpinan pada sebuah perusahaan besar yang memiliki banyak cabang di daerah, termasuk di perdalaman.
Sebagai pimpinan, anda perlu mendengar laporan dari bawahan anda. Salah satu bawahan anda yang ada di pedalaman, suatu ketika memberikan laporan yang mengejutkan. Isi laporannya sebagai berikut. Telah terjadi tindakan yang memalukan karena seratus persen wanita yang ada di perusahaan melakukan seks bebas hanya kepada 1 orang laki-laki.
Apa reaksi anda sebagai pimpinan? Sebagai pimpinan yang memahami statistika, Anda tentunya tidak akan percaya begitu saja dan mencoba menggali informasi lebih jauh. Ternyata laporan yang disampaikan memang benar, bahwa 100% wanita yang ada di perusahaan melakukan seks bebas hanya kepada satu orang laki-laki. Data yang benar, namun dimanfaatkan secara salah. Setelah diteliti, ternyata jumlah wanita yang bekerja di perusahaan di pedalaman itu haya berjumlah 1 orang sehingga secara persentase, data tersebut memang menunjuk jumlah 100%.
Dari kedua contoh yang ada, kita akhirnya menjadi sadar, bahwa banyak ruang untuk memanipulasi data, dan agar kita tidak mudah terjebak, kita perlu mempelajari statistika.
2. Pemanfaatan Statistika
Apakah anda mengikuti proses pelaksanaan jajak pendapt pada saat pemilihan presiden tahun 2014? Berbagai lembaga berlomba melakukan suatu proses hitug cepat untuk memprediksi siapakah yang akan menjadi presiden berikutnya.
Gambaran ini menunjukkan salah satu pemanfaatan statistika. Betapa kuatnya statistika dalam memengaruhi kehidupan manusia sehingga ketika terjadi perbedaan maka masing-masing berusaha mempertahankan kredibilitasnya. Kondisi ini menunjukkan bagaimana statistika dapat memberikan dampak yang luas pada manusia. Selain menggambarkan manfaat statistika, proses hasil hitung cepat ini juga menunjukkan bagaimana statistika dimanipulasi untuk kepentingan tertentu. Kita coba lihat kejadian yang ada dalam proses hasil hitung cepat dalam pemilihan presiden tahun 2014.
Bisa dilihat hasil survei 12 lembaga survei, ada 8 lembaga survei yang menghasilkan perhitungan cepat yang relatif sama, sekitar 52% untuk Jokowi dan 48% untuk Prabowo. Sementara 4 lembaga survei memenangkan Prabowo. Dari 4 lembaga survei, hanya satu yang hasil hitung cepatnya menunjukkan perbedaan signifikan antara suara Jokowi dan Prabowo, yaitu hasil perhitungan cepat PUSKAPTIS. hasil perhitungan cepat PUSKAPTIS menunjukkan Prabowo mendapat 52% suara dan Jokowi mendapat 48%. Selisih persentase jumlah suara sekitar 4%, dengan margin error +/- 1% maka selisih terendah antara suara Prabowo dan Jokowi adalah (52%-1%=51%) - (48%+1%=49%) = 2%. Sementara hasil perhitungan cepat 3 lembaga lain, selisih persentase suara masih berada di dalam margin error sehingga dengan metode uji statistik, tidak bisa disimpulkan bahwa ada perbedaaan yang signifikan jumlah suara antara kedua kubu.
Selain banyak dimanfaatkan di kalangan politik, di kalangan bisnis statistika juga memegang peranan yang sangat penting. Perusahaan di manapun selalu mengandalkan pada statistika dalam proses pengambilan keputusan. Baik perushaan berskala besar maupun perusahaan berskala kecil mengandalkan pada statistika. Dan bukan hanya sektor ekonomi dan politik, dalam setiap segi kehidupan manusia, semua mengandalkan pada statistika. Bahkan dalam kehidupan manusia yang sedrhana pun, baik secara sadar maupun tidak sadar mengandalkan pada statistika.
Pernakah anda ragu-ragu, apakah hari ini akan hujan atau tidak? Ketika anda sampai pada kesimpulan, hari ini akan hujan, Anda akan membawa payung maka anda juga sudah menerapkan statistika. Dengan kata lain, semua orang secara sadar atau tidak sadar sudah memanfaatkan statistika, dari hal yang sangat sederhana sampai hal yang sangat kompleks.
B. KLASIFIKASI STATISTIKA
Untuk mempermudah kita dalam memakai statistika, kita perlu membuat beberapa klasifikasi statistika. Ada dua klasifikasi yang kita gunakan, yaitu pertama berdasarkan pada kativitas yang dilakukan, kedua berdasar pada metodenya.
1. Berdasarkan aktivitas yang dilakukan.
a. Statistika deskriptif; membahas tentang cara-cara pengumpulan data, penyederhanaan angka pengamatan yang diperoleh, serta melakukan ukuran pemusatan dan penyebaran untuk memperoleh informasi yang menarik, berguna, dan mudah dipahami.
Dengan kata lain, statisti deskrptif adalah penggambaran data yang telah dikumpulkan. Banyak cara yang bisa digunakan untuk menggambarkan data, bisa menggunakan tabel distribusi, grafik, diagram, atau dalam bentuk narasi.
Contoh statistika deskriptif :
b. Statistika Inferensia; Cara menganalisis data serta mengambil kesimpulan (terkait dengan estimasi parameter dan pengujian hipotesis). Statistika inferensia berkaitan dengan analisis sebagian data sampai ke peramalan atau penarikan kesimpulan mengenai kesleuruhan data. Berikut Contoh statsitika inferensia :
Meski dianggap gagal menciptakan perubahan dalam meningkatkan kesejahteraan rakyat, otonomi daerah masih tetap didukung oleh mayoritas masyarakat Indonesia (73%), hanya 27% yang menyatakan menolak otonomi daerah. Jumlah sampel 1240, dengan margin of error +/- = 3,0% pada tingkat kepercayaan 95%. Responden tersebar di 33 provinsi dengan jumlah responden yang proporsional sesuai dengan jumlah penduduk di masing-masing provinsi.
2. Berdasarkan Metodenya
a. Statistika parametrik; bagian dari statistika inferensia yang mempertimbangkan nilai dari satu atau lebih parameter populasi, seperti rata-rata hitung, standar deviasi, dan korelasi. Karakteristik dari parametrik antara lain memperhitungkan nilai yang ada di populasi, datanta berskala minimal interval, bentuk variabelnya kontinu, serta datanya terdistribusi secara normal. Contoh dari statistika parametrik antara lain : uji t, uji z, serta korelasi pearson.
a. Statistika nonparametrik; bagian dari statistika inferensia yang tidak memperhatikan nilai dari satu atau lebih parameter populasi. Karakteristik dari nonparametrik antara lain datanya berskala ukur nominal atau ordinal, variabelnya diskret, dan biasanya untuk menguji sampel yang relatif kecil (kurang dari 30). Contoh dari statistika non-parametrik anatara lain uji chi square, uji wilcoxon, serta uji spearmen.
KEGIATAN BELAJAR 2 :
KONSEP DASAR STATISTIKA DAN SKALA PENGUKURAN
A. KONSEP DASAR STATISTIKA
Ketika anda mempelajari KB 1, tentunya anda membaca beberapa konsep yang muncul dalam penjelasan materi statistika. Agar kita memiliki pemahaman yang sama tentang konsep tersebut, ada baiknya dalam KB 2 ini, kita bersama-sama mempelajari beberapa konsep dasar yang ada dalam statistika,
1. Variabel
Variabel bisa kita artikan sebagai atribut dari kelompok objek yang diteliti dengan variasi dari masing-masing objeknya. Dengan kata lain, variabel merupakan sebuah konsep yang memiliki variasi nilai. Variasi nilai dari sebuah variabel, kita sebut sebagai kategori. Kita ambil contoh berikut; Pendidikan merupakan sebuah variabel yang memiliki variasi nilai (kategori) tinggi, sedang, dan rendah. Contoh lain; misalnya jenis kelamin, dengan kategori laki-laki dan perempuan. Masih banyak contoh variabel yang ada di sekitar kita, mulai dari sederhana hingga yang sangat kompleks.
Seperti halnya ketika kita mencoba mengklasifikasi statistika maka variabel bisa kita klasifikasi berdasar beberapa bentuk klasifikasi
a. Klasifikasi yang pertama adalah berdasarkan bulat atau tidaknya nilai yang diperoleh. Variabel kita bedakan menjadi variabel diskret dan variabel kontinu.
1). Varibel Kontinu ; adalah variabel yang besar nilainya dapat menempati semua nilai yang berada diantara dua titik. Nilai yang berada diantara dua titik bisa berbentuk nilai bulat atau nilai pecahan. Contoh berat gula pasir, dengan variasi nilai 2 kg, 2,5 kg., 3,7 kg. dan seterusnya. Contoh lain indeks prestasi kumulatif (IPK) dengan variasi nilai 2; 2,5; 3,75; dan seterusnya.
2). Variabel diskret ; adalah variabel yang besarnya tidak dapat menempati semua nilai. Nilai bilangan diskret selalu berupa bilangan bulat. Contoh: jumlah mahasiswa yang terdaftar dalam tutorial online, variasi nilainya 15, 20, 50, dst. Contoh lain jumlah kendaraan yang diparkir pada hari Minggu, variasi nilainya 12, 24, 40, dst. Jika kita cermati, dalam variabel diskret tidak mungkin mengandung pecahan, misalnya tidak mungkin kita akan menemukan 4,5 mahasiswa, atau kita akan menemukan 20,3 mobil.
b. Kalsifikasi yang kedua berdasarkan bentuk angka atau tidaknya nilai yang diperoleh. Dalam klasifikasi ini, variabel kita bedakan menjadi variabel kuantitatif dan variabel kualitatif.
1). Variabel kuantitatif adalah variabel yang variasi nilainya dalam bentuk angka. Contoh dari variabel kuantitatif antara lain usia dengan variasi nilai 15 tahun, 20 tahun, dst. Contoh lain adalah jumlah konsumsi buah dalam seminggu dengan variasi nilai 3 buah, 5 buah, dst.
2). Variabel Kualitatif adalah variabel yang variasi nilainya tidak dalam bentuk angka. Contoh dari variabel kualitatif antara lain jenis kelamin dengan variasi nilai laki-laki dan perempuan. Contoh lain lokasi tempat tinggal mahasiswa, dengan variasi nilai Jawa, Sumatera, Kalimantan, dst.
Pengklasifikasian variabel bisa kita buat dalam bentuk bagan berikut :
2. Data
Merupakan sejumlah informasi yang dapat memberikan gambaran tentang suatu keadaan. Syarat data antara lain :
a. harus sesuai dengan kenyataan yang sebenarnya (memiliki akurasi yang tinggi)
b. harus bisa mewakili parameter yang diukur dengan variasi yang kecil
c. harus relevan untuk menjawab suatu persoalan yang menjadi pokok bahasan
d. harus tepat waktu.
Informasi yang ada pada umumnya diperoleh melalui observasi (pengamatan) yang dilakukan terhadap sekumpulan individu, sekelompok orang, dan berbagai objek lainnya. Informasi yang diperoleh dapat memberikan keterangan, gambaran, atau fakta mengenai suatu persoalan baik dalam bentuk kategori, maupun huruf atau bilangan. Seperti halnya variabel, Data juga sebaliknya kita buat dalam beberapa klasifikasi sebagai berikut :
a. Berdasarkan metode pengumpulan, data dibedakan menjadi :
1). Data Primer ; data yang didapat dari sumber pertama, biasanya melalui wawancara langsung atau melalui pengisian kuesioner;
2). Data Sekunder ; data yang didapat dari sumber kedua dan seterusnya, biasanya data ini merupakan data yang sudah diolah lebih lanjut. Contohnya data BPS, data yang ada dalam jurnal, buku, serta majalah.
b. Berdasarkan sifatnya, data dibedakan menjadi :
1). Data Kualitatif ; data yang sifatnya hanya menggolongkan saja, atau dengan kata yang lain data yang ada hanya bisa digunakan untuk membedakan saja antara data satudengan data lainnya. Biasanya data ini memiliki skala ukur nominal dan ordinal. Contoh data tentang jenis kendaraan, persepsi mahasiswa, serta lokasi tempat tinggal.
2). Data Kuantitatif ; data yang sifatnya tidak hanya menggolongkan saja, namun juga bisa menunjukkan bobot perbedaan antara data satu dengan data lainnya. Data ini berbentuk angka. Contoh data tentang besaran penghasilan, usia, serta jumlah kekayaan.
c. Berdasarkan sumbernya, data dibedakan menjadi :
1). Data Internal ; data yang didapat didalam kelompok atau organisasi dan menggambarkan keadaan yang ada dalam kelompok atau organisasi tersebut. Contoh data tentang jumlah dosen yang ada di FISIP UT.
2). Data Eksternal ; data yang didapat dari luar kelompok atau organisasi dan menggambarkan keadaan yang ada di luar kelompok atau organisasi tersebut. Contoh data tentang jumlah perguruan tinggi terakreditasi yang ada di DIKTI.
d. Berdasarkan waktu pengumpulan, data dibedakan menjadi :
1). Data time series ; data yang dikumpulkan dari beberapa tahapan waktu yang terjadi secara kronologis. Contoh data jumlah mahasiswa yang registrasi dari tahun 2009 hingga tahun 2014
2). Data cross section ; data yang dikumpulkan pada waktu tertentu saja. Contoh data jumlah mahasiswa yang registrasi pada semester 2014.1.
Pengklasifikasian data dapat dibuat dalam bentuk bagai sebagai berikut :
B. SKALA PENGUKURAN
Skala bisa kita artikan sebagai perbandingan antarkategori dari sebuah objek yang memiliki nilai berbeda. Dengan demikian, skala yang dimaksud di sini merujuk pada variabel. Jika kita cermati pengertian tentang skala maka kita harus memastikan bahwa ketika kita menentukan skala dari sebuah variabel, harus didasarkan pada kategori yang melekat dalam variabel tersebut.
Dengan kata lain, sebuah variabel bisa memiliki skala yang berbeda-beda bergantung pada kategori yang melekat didalamnya. Contoh variabel penghasilan, kita bisa kategorikan penghasilan kedalam kategori tinggi, sedang dan rendah. Dan kita bisa kategorikan penghasilan ke dalam 5 juta, 7 juta, atau 10 juta. Dengan kategori yang berbeda sekalipun variabelnya sama, membuat variabel tersebut bisa kita klasifikasikan dalam skala yang berbeda.
Sementara itu, pengukuran bisa kita artikan sebagai dasar yang digunakan dalam setiap metode ilmiah. Dari kedua pengertian skala dan pengukuran tersebut, kita bisa artikan skala pengukuran semacam kesepakatan yang digunakan sebagai acuan untuk mennentukan nilai yang ada pada alat ukur sehingga ketika kita menggunakan alat ukur tersebut, akan menghasilkan data yang sama dalam setiap kesempatan.
Dalam statistika dikenal adanya empat skala; yaitu skala nominal, skala ordinal, skala interval, dan skala rasio. Skala pengukuran ini menjadi penting karena skala yang berbeda akan menentukan uji statistik yang akan digunakan.
1. Skala Nominal
Skala nominal merupakan skala yang melekat pada variabel yang kategorinya hanya bisa digunakan untuk membedakan antara satu kategori dengan kategori lainnya. Kita tidak bisa mengatakan bahwa kategori yang satu lebih baik dari kategori yang lain, atau kategori yang satu lebih tinggi dari kategori yang lain. Dengan demikian, skala nominal ini biasanya berupa variabel dengan data kualitatif.
Dalam kegiatan penelitian, kita bisa saja memberikan angka pada kategori dalam variabel berskala nominal, namun angka yang ada tidak bisa dijadikan dasar untuk menentukan bobot dari kategori karena angka yang ada hanya bisa digunakan untuk membedakan antarkategori. Tidak adanya bobot yang bisa ditunjukkan angka yang digunakan, membuat kita bisa saja mengganti anka yang ada dengan sembarang angka. Contoh yang paling umum adalah variabel jenis kelamin dengan kategori laki-laki dan perempuan. Kita hanya bisa membedakan bahwa yang satu adalah laki-laki dan yang lain adalah perempuan dan tidak bisa mengatakan bahwa laki-laki lebih baik dari perempuan atau sebaliknya.
Kita bisa memberikan angka untuk setiap kategori yang ada, misalnya angka 1 untuk laki-laki dan angka 2 untuk perempuan, namun demikian sekali lagi bahwa angka 2 tidak bisa diartikan memiliki bobot yang lebih baik dibanding angka 1 sehingga tidak menjadi masalah ketika ingin mengubah angka tersebut, misalnya angka 1 untuk perempuan dan angka 2 untuk laki-laki.
Contoh lainnya adalah variabel agama dengan kategori Islam, Katolik, Hindu, Budha, Kristen, serta Aliran Kepercayaan. Angka yang digunakan dalam skala nominal hanya berfungsi sebagai kode yang memiliki arti berbeda dengan angka tersebut.
2. Skala Ordinal
Skala ordinal merupakan skala yang melekat pada variabel yang kategorinya selain menunjukkan adanya perbedaan, juga menunjukkan adanya tingkatan yang berbeda. Dengan demikian, dalam skala ordinal kita bisa menunjukkan bahwa kategori yang satu lebih baik dari kategori yang lain, atau kategori yang satu lebih tinggi dari kategori yang lain, dan tentunya termasuk didalamnya, yaitu kategori yang satu berbeda dengan kategori yang lain. Dengan kata lain, skala ordinal mencakup pula karakteristik yang ada dalam skala nominal.
Contoh variabel yang berskala ordinal adalah penghasilan dengan kategori tinggi, sedang, dan rendah. Contoh variabel lain adalah jabatan dengan kategori direktur, manajer, dan staf. Kategori yang ada dalam kedua variabel tersebut, jelas menunjukkan adanya bobot yang berbeda sehingga kita bisa katakan bahwa orang yang penghasilannya tinggi memiliki tingkatan yang lebih baik dibanding orang yang memiliki penghasilan rendah, demikian pula jabatan direktur, tentunya memiliki tingkatan yang lebih baik dibandingkan jabatan staf.
Seperti halnya dalam skala nominal, dalam skala ordinal kita juga memanfaatkan angka-angka untuk menggambarkan kategori yang ada. Dalam skala ordinal, angka yang digunakan selain untuk membedakan juga untuk menunjukkan bobot yang berbeda sehingga jika dalam skala ordinal kita harus memperhatikan bobotnya.
Contoh penghasilan dengan kategori tinggi, sedang, dan rendah, kita beri kode 1 rendah, 2 sedang, 3 tinggi. Kode itu tidak bisa kita ubah menjadi 1 tinggi, 2 rendah, 3 sedang. Angka yang tidak bisa sembarang diubah terjadi karena angka tersebut juga menunjukkan adanya tingkatan yang berbeda, bahwa 2 tentunya lebih besar dari 1, dan 3 lebih besar dari 2. Persamaan adalah baik skala nominal maupun di skala ordinal, angka yang digunakan berfungsi sebagai kode yang memiliki arti yang berbeda dengan angka tersebut.
3. Skala Interval
Skala Interval merupakan skala yang melekat pada variabel yang kategorinya selain menunjukkan adanya perbedaan, juga menunjukkan adanya perbedaan, juga menunjukkan adanya tingkatan yang berbeda, dan juga menunjukkan adanya rentang nilai.
Dengan demikian, dalam skala interval kita bisa menunjukkan bahwa kategori yang satu lebih baik dari kategori yang lain, atau kategori yang satu lebih tinggi dari kategori yang lain, dan kategori yang satu berbeda dengan kategori yang lain, namun juga kita bisa menunjukkan bahwakategori yang satu memiliki rentang nilai dari sekian sampai sekian, dan kategori lainnya memiliki rentang nilai dari sekian sampai sekian.
Dengan kata lain, skala interval mencakup pula karakteristik yang ada dalam skala nominal dan skala ordinal. Contoh variabel yang berskala interval adalah jarak tempuh dengan kategori 0 sampai 25 km, 25 km sampai 50 km, dan 50 km sampai 75 km. Contoh variabel lain adalah lamanya penerbangan dengan kategori 1 sampai 2 jam, kategori 2 sampai 3 jam. Kategori yang ada dalam kedua variabel tersebut, jelas menunjukkan adanya bobot yang berbeda sehingga kita bisa katakan bahwa kendaraan yang memiliki jarak tempuh 0 sampai 25 km memiliki jarak tempuh yang lebih sedikit, dibandingkan kendaraan dengan jarak tempuh 25 sampai 50 km. Namun demikian, kita tidak bisa mengatakan bahwa kendaraan dengan jarak tempuh 25 sampai 50 km memiliki jarak tempuh dua kali dibanding kendaraan dengan jarak tempuh 0 sampai 25 km.
4. Skala Rasio
Skala rasio merupakan skala yang melekat pada variabel yang kategorinya selain menunjukkan adanya perbedaan, juga menunjukkan adanya tingkatan yang berbeda, menunjukkan adanya rentang nilai, serta bisa diperbandingkan.
Nilai yang ada bisa diperbandingkan karena adanya nol mutlak, yang bisa diartikan bahwa setiap angka memulai dari titik nol yang sama. Dengan demikian, dalam skala rasio kita bisa menunjukkan bahwa kategori yang satu lebih baik dari kategori yang lain, atau kategori yang satu lebih tinggi dari kategori yang lain, dan kategori yang satu berbeda dengan kategori yang lain, namun juga kita bisa menunjukkan bahwa kategori yang satu memiliki rentang nilai dari sekian sampai sekian, dan kategori lainnya memiliki rentang nilai dari sekian sampai sekian.
Kita bisa juga mengatakan bahwa 8 adalah dua kalinya 4, atau 10 adalah lima kalinya 2. Dengan kata lain, skala rasio mencakup pula karakteristik yang ada dalam skala nominal, skala ordinal, dan skala interval.
Contoh variabel yang berskala rasio adalah penghasilan, dengan kategori 5 juta, 10 juta, dan 15 juta. Contoh lain berat badan dengan kategori 32 kg, 64 kg, dan 75 kg. Jika kita perhatikan kategori dari variabel berskala rasio, kita bisa perbandingkan antara kategori satu dengan yang lain. Orang yang berat badannya 64 adalah dua kali berat badan orang yang beratnya 32 kg. Demikian pula orang yang penghasilannya 10 juta adalah dua kalinya dari orang yang penghasilannya 5 juta. Kita bisa memperbandingkan nilai yang ada karena kedua kategori tersebut dimulai dari titik nol yang sama. Kita coba lihat ilustrasi berikut :

Kalau kita bandingkan antara skala rasio dan skala nominal maupun ordinal, mereka memiliki kesamaan, yaitu menggunakan angka-angka. Bedanya angka yang digunakan dalam skala nominal dan ordinal hanya merupakan kode, bukan arti dari angka itu sendiri, misalnya 1 bukan berarti "satu", tetapi artinya "laki-laki" atau 2 bukan berarti "dua" tetapi artinya "perempuan". sedangkan dalam skala rasio, angka yang ada merupakan arti dari angka itu sendiri, jadi kalau ditunjukkan angka 15 diartikan sebagai "lima belas".
Secara skematis, skala dan karakteristiknya terlihat dalam skema berikut :
MODUL 2 :
PENYAJIAN DATA
Data yang telah dikumpulkan dalam suatu penelitian harus disusun dan disajikan dalam bentuk mudah untuk dipahami. Penyusunan dan penyajian data ini, akan membantu pihak-pihak yang terkait dengan hasil penelitian yang kita lakukan. Hal ini menjadi penting terutama apabila jumlah data yang kita kumpulkan sangat banyak. Selain untuk kepentingan analisis, penyusunan dan penyajian data ini juga untuk memudahkan orang lain melihat hasil penelitian kita.
Penyajian data dapat dikelompokkan menjadi penyajian data untuk data kualitatif dan penyajian data untuk data kuantitatif. Pembagian ini didasarkan pada penentuan dari skala variabel. Ada empat macam skala yaitu nominal, ordinal, interval, dan rasio. Penyajian data dengan skala nominal dan ordinal lebih bersifat kualitatif, sedangkan penyajian data dengan skala interval dan rasio bersifat kuantitatif.
Data yang kita kumpulkan dalam suatu penelitian dapat berupa nagka-angka ataupun informasi-informasi tertentu. Angka-angka atau informasi-infornasi tersebut, harus kita sederhanakan terlebih dahulu. Angka-angka kita masukkan dalam kategori kelas-kelas interval, misalnya usia responden kita susun dalam interval kelas 21-30, 31-40, dan 41 - 50. Sementara itu, informasi yang kita peroleh kita klasifikasikan dalam kategori-kategori tertentu, misalnya jenis kelamin responden kita kategorikan ke dalam laki-laki dan perempuan. Data tersebut kemudian kita sususn berdasarkan klategori-kategori tersebut. Susunan tersebut dikenal dengan istilah
tabel frekuensi. Tabel Frekuensi memiliki komponen-komponen sebagai berikut :
Seperti terlihat dalam contoh tabel diatas, suatu tabel harus ada hal seperti berikut ini :
1. No. tabel; Nomor tabel ini untuk mempermudah pengidentifikasian jumlah tabel yang ada dalam suatu karya ilmiah. Untuk setiap bab bisa dimulai dengan angka awal sehingga untuk bab satu, nomor tabel yang digunakan I.1, I.2, I.3, dst. Untuk Bab dua digunakan II.1, II.2, II.3, dst.
2. Judul tabel; Pemebrian judul dimaksudkan untuk mempermudah pembaca membandingkan antara satu tabel dengan tabel lain.
3. Jumlah Data; Dalam tabel biasanya digunakan notasi N = ..... . Jumlah data ini juga ditampilkan untuk mempermudah pembaca mengetahui secara cepat beberapa jumlah data, atau biasanya dalam hal ini jumlah responden.
4. Kolom pertama dari suatu tabel umumnya berisikan Kategori; Kategori ini dapat berupa angka, dapat pula berisikan informasi penggolonggan. Kategori yang bukan berupa angka merupakan ciri penyajian data kualitatif, sedangkan kategori yang berupa angka merupakan ciri penyajian data kuantitatif. Kategori pada setiap kelas tidak boleh tumpang tindih. Hal ini dimaksudkan agar setiap informasi yang ada dapat dimasukkan ke dalam salah satu kelas.
5. Kolom kedua dari suatu tabel adalah frekuensi; Frekuensi menunjukkan berapa banyak kategori yang ada dipilih oleh responden. Frekuensi ini yang digunakan untuk menentukan persentase dari setiap kategori.
6. Kolom selanjutnya adalah kolom persentase; Persentase ini menunjukkan proporsi dari frekuensi setiap kelas. Cara mendapatkannya adalah frekuensi setiap kelas dibagi banyak data, kemudian dikali 100%.
7. Sumber data dan Keterangan harus dicantumkan; Sumeber data ini berguna untuk membetulkan kembali, jika terjadi kesalahan data. Selain itu, untuk menghindari penggunaaan data kepunyaaan orang lain.
Selain menggunakan tabel frekuensi, data dapat juga disajikan dengan menggunakan diagram. Diagram membuat penyajian data menjadi lebih menarik dan perbandingan setiap kategori lebih mudah terlihat. Diagram ini dapat dibuat dari data yang belum tersusun maupun dari data yang sudah tersusun dalam tabel frekuensi.
Untuk membuat sebuah diagram, kita harus memperhatikan hal-hal berikut ini :
1. Suatu diagram seharusnya berisi mengenai keseluruhan informasi data yang disajikan sehingga pembaca tidak perlu lagi mencari informasi untuk memahami diagram di dalam teks.
2. Seperti halnya tabel frekuensi, diagram juga harus memiliki nomor diagram, judul, serta jumlah data. Bedanya, nomor dan judul diagram diletakkan dibawah diagram.
3. Untuk data interval rasio angka dari setiap kategori harus jelas terlihat. Bila data disederhanakan maka ukuran yang digunakan harus jelas terlihat. Data disajikan dalam ukuran jutaan maka 10 juta harus tertulis 10, sedangkan 500 ribu harus tertulis 0,5 juta. Keterangan ukuran ini biasanya ditampilkan di bagian bawah diagram.
Penyajian data yang dilakukan dengan menggunakan diagram atau grafik memiliki kelebihan dibanding dengan menggunakan tabel frekuensi, namun juga da kelemahannya. Kelebihan dan kelemahan penggunaaan grafik dapat kita lihat dalam tabel berikut :
KEGIATAN BELAJAR 1 :
PENYAJIAN DATA KUALITATIF
Data Kualitatif umumnya dihasilkan dari pertanyaan-pertanyaan terbuka. Pertanyaan Terbuka adalah pertanyaan yang kategori jawabannya tidak dibatasi oleh si peneliti. Karena jawabannya tidak dibatasi maka akan banyak sekali alternatif jawaban. Sebagai contoh, "Mengapa anda mencri kerja di kota?" Jawaban dari pertanyaan ini bisa bermacam-macam di antaranya berikut ini.
1. Di kota lebih mudah mencari pekerjaan
2, Kota lebih menjanjikan karier tinggi
3. Kota lebih banyak peluang
4. Pekerjaan apapun dapat menghasilkan uang
5. Di desa terjadi kekeringan
6. Di desa terjadi gagal panen karena serangan hama
7. Di desa tidak ada pekerjaan yang sesuai dengan pendidikan.
Jawaban-jawaban di atas tentunya masih bisa bertambah. Apabila disajikan langsung maka akan ada jawaban yang sebenarnya sama, misalnya "di kota lebih mudah mencari pekerjaan", sama dengan jawaban "kota lebih banyak peluang", dan sama juga dengan jawaban "pekerjaan apa pun menghasilkan uang". Untuk itulah, semua alternatif jawaban yang sama perlu dikumpulkan kemudian dibuat suatu kategori baru seperti berikut ini :
Dari pengelompokan diatas maka kategori data menjadi lebih sedikit. Dari 7 kategori yang ada dapat kita sederhanakan menjadi 4 kategori, yaitu sebagai berikut :
1. Di kota mudah mendapatkan pekerjaan
2. Kota lebih menjanjikan karier tinggi
3. Keadaan alam di desa
4. Di desa tidak ada pekerjaan yang sesuai dengan pendidikan.
Pengurangan kategori ini tentunya akan mempermudah kita dalam menginterpretasikan data yang ada. Satu hal yang perlu diperhatikan dalam penyederhanaan data ini adalah dalam proses penggabungan yang dilakukan, tidak boleh menghilangkan informasi yang ada seperti sebelum proses penggabungan dilakukan.
A. PENYAJIAN DAN INTERPRETASI DATA
Data kualitatif merupakan data yang memperhatikan karakteristik-karakteristik dari suatu objek penelitian. Oleh karena itu, data kualitatif tidak menampilkan kategori dalam bentuk angka. Penampilan dalam bentuk angka justru akan menghilangkan informasi yang dimiliki oleh data kualitatif.
Tingkatan pengukuran yang bisa diberikan untuk data kualitatif adalah skala nominal dan ordinal. Skala nominal akan mengklasifikasikan setiap data ke dalam kategori-kategori tertentu, sedangkan dengan skala ordinal akan didapatkan peringkat dari setiap kategori . Data kualitatif dapat disajikan dalam bentuk tabel dan diagram.
1. Penyajian dan Interpretasi Data dalam Bentuk Tabel frekuensi
Tabel yang digunakan untuk data kualitatif disebut dengan tabel distribusi frekuensi kualitatif. Ciri dari tabel untuk data kualitatif ini diperlihatkan pada pembagian kelas yang didasarkan oleh kategori-kategori tertentu. Sebagai contoh, kita akan coba melihat variabel Alasan Pemilihan Perguruan Tinggi.
Berdasarkan Tabel 2.1 maka kita bisa menginterprestasikan bahwa biaya pendidikan menjadi faktor penting dalam pemilihan perguruan tinggi, yaitu sebesar 32,14%. Faktor lainnya yang cukup signifikan menjadi alasan pemilihan perguruan tinggi adalah fasilitas belajar-mengajar, yaitu sebesar 25% dari kseleuruhan responden yang diteliti.
Tabel 2.1 merupakan contoh tabel dengan skala pengukuran nominal. Sekarang, marilah kita perhatikan contoh tabel dengan skala pengukuran ordinal. Perbedaan kedua tabel tentunya pada kategori. Kategori pada skala ordinal akan memperlihatkan adanya tingkatan, sedangkan pada skala nominal kategori yang ada hanya sekadar menggambarkan pengklasifikasian data. Contoh varibale skala ordinal adalah status sosial ekonomi responden.
Berdasarkan Tabel 2.2 ini kita bisa melakukan interprestasi bahwa sebagian besar responden memiliki status sosial ekonomi yang sedang, yaitu sebanyak 50%.
2. Penyajian dan Interpretasi Data dalam Bentuk Diagram
a. Diagram Lingkaran (Pie Chart)
Diagram lingkaran merupakan diagram yang dapat digunakan untuk semua tingkatan pengukuran. Pada diagram lingkaran ini, data yang ada digambarkan dalam bentuk lingkaran, di mana lingkaran tersebut dibagi atas sejumlah kategori yang ada. Untuk setiap kategori wilayah yang didapatnya didasarkan pada perhitungan sebagai berikut n/N x 360 derajat, dimana n adalah frekuensi tiap kategori atau kelas, dan N adalah jumlah keseluruhan data.
Rumus ini juga bisa diganti dengan rumus n/N x 100%. Kini kita coba gunakan tabel 2 untuk menghasilkan diagram lingkaran sebagai berikut.
Pada Diagram 2.1 terlihat bahwa yang paling banyak dikemukakan oleh mahasiswa dalam memilih perguruan tinggi adalah biaya pendidikananya yang tidak terlalu mahal, yaitu sebesar (33%).
Pada data yang terbagi dalam beberapa kategori yang cukup banyak dan setiap kategori memiliki frekuensi yang hampir sama maka diagram lingkaran kurang dapat menun jukkan tingkatan setiap kategori. Banyaknya kategori dianjurkan tidak lebih dari 7 karena akan sulit untuk membandingkan perbedaan (besar-kecilnya) tiap bagian kategori atau frekuensi. Kita coba perhatikan diagram lingkaran yang memiliki kategori yang banyak sebagai berikut. Anda tentunya akan sulit untuk membedakan setiap kategorinya.
b. Diagram Batang (Bar Graph)
Pada diagram batang setiap kategori diwakilkan oleh suatu persegi panjang, dimana tinggi dari setiap persegi panjang ditentukan oleh frekuensi masing-masing kategori. Oleh karena itu, dalam diagram batang digunakan 2 macam sumbu, yaitu sumbu horizontal dan sumbu vertikal. Pada sumbu horizontal diletakkan kategori dari variabel, sedangkan sumbu vertikal merupakan frekuensi dari setiap kategori. Salah satu hal penting yang harus diperhatikan dalam membuat diagram batang adalah penempatan batang harus terpisah antara satu batang dengan yang lain. Mengapa demikian? Ingat bahwa skala yang digunakan adalah skala nominal dan ordinal yang bisa juga kita kelompokkan ke dalam variabel diskret. Masih ingat tentang variabel diskret? Kategori untuk variabel diskret meruapakan bentuk bilangan bulat sehingga dalam pembuatan batang juga harus terpisah, sehingga melambangkan sifatnya yang tidak mengandung pecahan. Untuk memberikan gambaran tentang sebuah diagram batang, kita gunakan lagi data yang ada pada Tabel 2.1.

B. PENYAJIAN DAN INTERPRETASI DATA MENGGUNAKAN SPSS
Dalam Ilmu Sosial kita bisa menggunakan program komputer dalam mengolah data. Di sini, kita akan melihat bagaimana tampilan yang disajikan jika kita menggunakan program SPSS. Untuk tampilan tabel frekuensi, kita lihat hasilnya sebagai berikut :
1. Tabel Frekuensi Hasil Pengolahan Data dengan SPSS

Kalau kita perhatikan tabel frekuensi yang ditampilkan dengan menggunakan program SPSS (Lihat Tabel 2.3) maka akan terlihat beberapa perbedaan seperti jumlah kolom yang ditampilkan. Pada kolom yang pertama, emnunjukkan kategori seperti halnya yang terdapat pada tabel frekuensai yang dibuat secara manual. Demikian pula kolom berikutnya, yaitu kolom frekuensi dan kolom persentase, memiliki kesamaan dengan kolom yang terdapat dalam tabel frekuensi secara manual. Kolom berikutnya sedikit berbeda, karena tidak ada pada tabel frekuensi manual. Kolom valid percent pada dasarnya sama dengan kolom percent, terutama pada hal perhitungannya, hanya saja dalam kolom percent, persentase dihitung dari keseluruhan responden yang ada, sedangkan dalam kolom valid percent sudah memperhitungkan missing value atau data yang dianggap hilang. Apa yang dimaksud dengan missing value atau data yang dianggap hilang? Data yang hilang terjadi karena, misalnya saja ada responden yang tidak menjawab pertanyaan yang diajukan sehingga dari seluruh responden yang ada, responden yang tidak menjawab tidak diperhitungkan dalam menghitung persentasenya. Kita mabil saja contoh dari tabel berikut ini yang memiliki missing value.

Coba Anda bandingkan antara Tabel 2.3 dan Tabel 2.4, terutama pada kolom percent dan valid percent. Bandingkan juga antara kolom percent dan kolom valid percent yang ada pada Tabel 2.4, maka Anda akan menemukan perbedaan angka.
Pada Tabel 2.3, kita belum memperhitungkan missing value, sementara Tabel 2.4 kita sudah memperhitungkan missing value . Kini kita bandingkan antara kolom percent dan valid percent yang ada pada Tabel 2.4. Pada kolom percent, responden yang tidak menjawab masih diperhitungkan dalam menghitung persentasenya, sedangkan pada kolom valid percent, responden yang tidak menjawab sudah tidak diperhitungkan lagi. Hal ini mengakibatkan persentase untuk responden yang memiliki status sosial ekonomi yang rendah, berbeda antara kolom percent dan valid percent .
Dalam analisis data, kita akan menggunakan kolom valid percent. Dengan demikian, berdasar Tabel 2.4 maka kita bisa menginterpretasikan bahwa sebagian besar responden memiliki status sosial ekonomi yang rendah (76,1%). Ingat yang digunakan adalah kolom valid percent. Kolom berikutnya menunjukkan akumulasi persentase yang didapat dengan menjumlahkan nilai yang ada dengan nilai sebelumnya. 76,1 % didapat dengan menjumlahkan nilai yang ada pada kategori rendah (76,1) dengan akumulasi nilai sebelumnya (0). 81,9% didapat dengan menjumlahkan nilai yang ada pada kategori sedang (5,8) dengan akumulasi nilai sebelumnya (76,1). Demikian pula nilai 100% didapat dengan menjumlahkan nilai yang ada pada kategori tinggi (18,1) dengan akumulasi nilai sebelumnya (81,9).
2. Diagram atau Grafik Hasil Pengolahan Data dengan SPSS
Seperti halnya tabel frekuensi, kita juga bisa menyajikan berbagai grafik dengan menggunakan program SPSS, dan hasilnya bisa kita lihat berikut ini :
Diagram Batang :
Pie Chart (Grafik Lingkran) :
KB 2 : PENYAJIAN DATA KUANTITATIF
Penggunaan skala pengukuran interval dan rasio akan menghasilkan data kuantitatif. Data kuantitatif ini berbentuk angka-angka, oleh karenanya kategori-kategori yang digunakan juga akan berbentuk angka. Penyajian data ini juga bisa dalam bentuk tabel dan diagram.
A. PENYEDERHANAAN DATA
Dalam pengumpulan data di lapangan, sering kali jawaban responden memiliki variasi jawaban yang sangat banyak sehingga jika kita tampilkan apa adanya maka data tersebut sulit untuk kita analisis. Langkah yang kita bisa lakukan adalah data tersebut harus dikelompokkan kedalam kelompok-kelompok angka. Pengelompokan angka-angka ini dinamakan dengan istilah kelas, sedangkan rentang antara satu angka dengan angka lainnya dinamakan dengan interval kelas. Proses ini disebut dengan penyederhanaan data atau pengelompokkan data. Salah satu cara yang bisa dilakukan adalah dengan menggunakan Kaidah Sturgess.
Langkah yang harus dilakukan adalah sebagai berikut :
Langkah Pertama :
Kita akan mencari nilai pengamatan yang terkecil dan yang terbesar dari pengamatan. Kemudian kita menentukan nilai L dan nilai H.
Nilai L diperoleh dengan cara mengurangi nilai pengamatan terkecil sebesar setengah unit (nilai pengamatan terkecil - 0,5).
Nilai H diperoleh dengan cara menambahkan nilai pengamatan terbesar sebesar setengah unit (nilai pengamatan terbesar + 0,5).
Dengan telah ditentukannya nilai L dan H maka kita dapat menghitung nilai Rentang (R) dengan rumus :
Range = (nilai observasi terbesar+0,5) - (nilai observasi terkecil-0,5)
Atau
R = H - L
Langkah Kedua :
Dalam penyajian data yang dikelompokkan, kita harus menentukan banyaknya kategori atau kelas yang akan dibuat. Untuk keseragaman dalam penentuan banyaknya kelas, dapat digunakan kaidah Sturgess. Dengan menggunakan kaidah sturgess banyak kategori atau kelas yang ditentukan dengan menggunakan rumus :
K = 1+(3,322xlog n)
dimana :
K = banyaknya kelas
n = jumlah data (observasi)
Hasil perhitungan jumlah kelas ini, akan selalu dibulatkan ke atas. Pembulatan ke atas ini, dimaksudkan agar semua data yang terkumpul dapat masuk dalam kategori atau kelas yang dibuat.
Langkah Ketiga :
Pada langkah ketiga, kita akan menentukan interval dari kategori atau kelas yang telah dibentuk. Interval kelas sangat dipengaruhi oleh banyaknya kelas dan penyebaran data yang akan disusun dalam distribusi frekuensi. Besar interval ini, dihitung dengan menggunakan rumus :
i = R = H - L
K K
dimana :
i = Interval Kelas
H = Nilai observasi yang tertinggi + 1/2 unit pengamatan terkecil
L = Nilai observasi yang terkecil - 1/2 unit pengamatan terkecil
K = Banyaknya kelas
Seperti halnya pembulatan dalam jumlah kelas maka hasil perhitungan interval kelas ini selalu dibulatkan ke atas, agar data yang terkumpul dapat tertampung.
Langkah Keempat
Langkah keempat ini merupakan langkah manakala kita mulai membuat tabel distribusi frekuensi. Tahap-tahap pembuatan tabel tersebut adalah :
a. Menentukan Batas Kelas Nyata dan Semu :
- Batas Kelas Nyata : Antara kelas tidak terdapat loncatan nilai (data kontinu)
- Batas Kelas Semu : Antara kelas terdapat loncatan nilai (data diskret)
b. Menentukan Nilai Tengah Kelas (x₁)
- Menggunakan batas kelas nyata
- Menggunakan batas kelas semu
c. Menentukan Frekuensi Absolut (f₁)
Besaran yang menunjukkan jumlah objek yang masuk dalam kelas yang bersangkutan dengan cara memasukkan atau mengelompokkan data observasi yang ada.
d. Menentukan Frekuensi Relatif (f rel)
Besaran yang menunjukkan persentase objek yang termasuk dalam kelas yang bersangkutan
Jika kita sudah mengetahui langkah-langkah yang harus dilakukan untuk menyederhanakan data dan juga menampilkannya dalam bentuk tabel frekuensi yang lengkap maka kini kita coba melakukan penyajian data untuk kasus mengenai skor yang didapatkan oleh 80 responden. Kepada 80 orang tersebut, kita tanyakan berapa skor yang mereka dapatkan. Data yang terkumpul adalah sebagai berikut ini. Data ini sering kali kita sebut dengan data yang tidak dikelompokkan atau data mentah (data yang belum diolah).
Berdasarkan data yang ada ini, kita lakukan langkah-langkah berikut :
1. Menentukan banyaknya kelas.
Banyaknya data (n) dalam kasus skor tes anak-anak adalah 80. Apabila dimasukkan ke dalam rumus sturgess banyaknya kelas akan dihasilkan sebagai berikut :
K = 1 + 3,322 log n
= 1 + 3,322 log 80
= 1 + 3,322 (1,90)
= 1 + 6,312
= 7,312
Nilai 7,312 memberikan petunjuk banyaknya kelas yang dapat dibuat adalah 7,312. Ingat bahwa pembulatan yang dilakukan harus ke atas sehingga kelas yang dibutuhkan adalah 8 kelas.
2. Menentukan interval kelas yang akan digunakan
Apabila diperhatikan data mengenai skor anak-anak, didapat data yang terendah adalah 33, sedangkan data tertinggi adalah 98. 33, harus kita kurangi dengan 0,5 menjadi 32,5 dan nilai 98, harus kita tambah dengan 0,5 menjadi 98,5. Selisih kedua angka ini adalah 66.
Interval kelas akan didapat dengan membagi nilai selisih angka tertinggi dan terendah dengan banyaknya kelas. Untuk contoh diatas maka akan didapatkan interval kelas sebebsar 66 : 8 = 8,25. Interval yang digunakan tidak 8, melainkan 9. Pembulata keatas dimaksudkan agar semua angka yang terdapat dalam data dapat tertampung.
Banyaknya kelas dan interval kelas berguna dalam mengelompokkan data yang ada. Banyak kelas 8 menunjukkan akan ada 8 kelas atau 8 pengelompokkan, sedangkan interval 9 menunjukkan akan ada 9 nilai pengamatan dalam setiap kelas.
Dengan demikian, nilai pengamatan yang terdapat dalam kelas pertama dari data di atas adalah 33, 34, 35, 36, 37, 38, 39, 40, 41. Kelas-kelas lainnya dapat dilihat dalam Tabel 2.7.
Kolom frekuensi didapatkan dengan menjumlahkan munculnya nilai di dalam daftar tes anak. Frekuensi pada kelas pertama (33-41) didapat dari :
33 =1
34 = 0
35 = 0
36 = 0
37 = 0
38 = 2
39 = 1
40 = 0
41 = 0
= 4
Jumlah kemunculan setiap nilai pengamatan pada kelas pertama di atas adalah 4.
Cara lain yang dapat digunakan adalah membuat turus untuk masing-masing kelas, yaitu sebagai berikut :
B. PENYAJIAN DAN INTERPRETASI DATA
1. Tabel Frekuensi
Tabel untuk data kuantitatif disebut dengan tabel distribusi frekuensi kuantitatif. Pembagian kelas pada tabel ini, ditentukan oleh angka-angka yang didapat dalam pengumpulan data. Apabila angka yang muncul tidak terlalu bervariasi maka tabel yang dibuat dapat berbentuk tunggal. Misalnya variabel jumlah anak dalam keluarga.
Berdasarkan Tabel 2.8 kita bisa menginterpretasikan bahwa jumlah anak yang dimiliki cukup bervariasi dan tidak terlihat kecendrungan apakah jumlah anak cenderung banyak atau sedikit. Hal ini dikarenakan persentase yang memiliki jumlah anak 2 (30%) relatif sama dengan keluarga yang memiliki jumlah anak 5 (25%).
Untuk data yang memiliki variasi sangat banyak maka kita lakukan pengelompokan data, seperti yang sudah kita pelajari dalam materi sebelumnya. Berdasarkan Tabel 2.8 maka kita bisa menginterpretasi bahwa sebanyak 24% anak kemampuannya cukup baik karena memiliki nilai tes antara 69 hingga 77, sedangkan yang memiliki skor di bawah 50 hanya 11%.
2. Diagram (Grafik)
a. Histogram
Diagram ini memiliki kesamaan dengan diagram batang. Hanya saja untuk histogram setiap persegi panjang tidak saling terpisah, tetapi saling menempel. Mengapa demikian? masih ingat tentang penjelasan batang yang harus terpisah dalam bar graph? Dalam Histogram, setiap batang harus saling menempel karena data yang digunakan bersifat kontinu. Dengan demikian, maka seluruh data yang ada harus masuk ke dalam kelas yang ada. Dengan saling menempelnya batang setiap kelas maka seluruh data yang ada akan masuk ke dalam kelas yang tersedia. Setiap persegi panjang (batang) diwakili oleh batas kelas nyata atau bisa juga dengan titik tengah kelas. Kita gunakan data yang ada pada Tbel 2.9 untuk memberikan gambaran tentang histogram.
Dari grafik 2.6 terlihat bahwa skor terbanyak yang dicapai anak-anak dalam penelitian tersebut adalah pada kelas 68,5 hingga 77,5 yaitu sebanyak 19 orang.
b. Poligon Frekuensi
Poligon frekuensi merupakan suatu grafik yang dihasilkan dengan menghubungkan puncak dari masing-masing nilai tengah kelas histogram. Dengan demikian, sumbu horizontalnya diwakilkan oleh angka titik tengah masing-masing kelas.
Pada diagram ini, poligon dimulai dan diakhiri pada sumbu horizontal (sumbu X) sehingga garis tidak menggantung, yaitu sebelum kelas pertama dan setelah kelas berakhir ditambahkan kelas dengan frekuensi nol (0). Titik tengah setiap kelas dapat diperoleh dengan cara menjumlahkan nilai terendah dan tertinggi masing-masing kelas kemudian dibagi dengan 2. Seperti pada kelas pertama; 32,5+41,5=74, Kemudian 74:2=37. Titik tengah kelas lainnya dapat kita lihat pada Tabel 2.9
Interpretasi dari diagram ini tidak terlalu berbeda dengan interpretasi pada histogram, hanya pada poligon frekuensi digunakan titik tengah. Skor tes anak paling banyak berada pada kelas dengan titik tengah 73.
c. Ogive
Ogive adalah suatu bentuk diagram yang dibuat dari frekuensi kumulatif. Pada Ogive, sumbu horizontalnya tidak menggunakan titik tengah, tetapi menggunakan batas nyata kelas atau kategori, sedangkan pada sumbu vertikalnya digunakan frekuensi kumulatif.
Garis yang menghubungkan batas kelas nyata selelu bergerak naik atau turun dan tidak mungkin naik turun. Titik awal dari garis ogive diwakili oleh batas kelas nyata bawah kelas pertama. Untuk mendapatkan frekuensi kumulatif, perhatikan Tabel 2.10. Frekuensi kumulatif bisa diartikan sebagai besaran yang menunjukkan jumlah objek yang termasuk kelas yang bersangkutan dan kelas-kelas sebelumnya.
Dari data pada Tabel 2.10 kita bisa hasilkan ogive, seperti pada diagram 2.8
d. Stem and Leaf Diagram (Grafik Batang Daun)
Diagram batang daun digunakan untuk memperoleh informasi mengenai distribusi dari gugus data dan nilai-nilai pengamatan aslinya. Diagram tersebut memuat semua data pengamatan yang ada dan hanya dapat digunakan pada data berskala rasio. Untuk menggambarkan batang dalam diagram ini ditulis bilangan-bilangan dan sebagai daunnya di sebelah kanan ditulis bilangan sisanya. Untuk memperoleh gambaran yang lebih jelas berikut ini terdapat beberapa tahapan yang dapat dilakukan untuk membuat diagram batang daun :
1) Pilih bilangan yang akan menjadi batang (perhatikan agar batang yang dipilih mencakuo semua bilangan dalam gugus data). Pada umumnya nilai batang dimulai dari 0 hingga 9
2) Urutkan batangnya. Tempatkan nilai batang terkecil di bagian atas dan nilai batang terbesar di bagian bawah (urutan dapat dibalik jika diinginkan yang sebaliknya).
3) Buat garis vertikal yang memisahkan batang dan daun
4) Untuk setiap nilai pengamatan, catat bilangan yang merupakan daun dari batang yang bersangkutan dan letakkan di sisi kanan batangnya
5) Susun urutan bilangan yang merupakan daun dari batang yang sama dalam urutan menarik.
Kita gunakan lagi data mentah yang menggambarkan skor tes anak :
Untuk mempermudah kita buat dulu data mentah tersebut ke dalam kolom berikut ini :
stem leaf
3 8893
4 98523
5 9614
6 3680370301875
7 609594280417103231625
8 881729042015083663
9 801385217103203
Setelah itu pada bagia leaf, kita urutkan dari data yang terkecil hingga terbesar sehingga menghasilkan diagram batang dan daun berikut :
C. PENYAJIAN DATA HASIL PENGOLAHAN DENGAN SPSS
Penyajian data untuk tabel frekuensi kuantitatif sama dengan penyajian data untuk tabel frekuensi kualitatif, untuk itu anda bisa melihat lagi contoh tabel frekuensi kualitatif. Untuk tampilan diagram hasil penyajian data dengan menggunakan program spss terlihat dalam diagram-diagram berikut :
Jika kita perhatikan stem and leaf yang sudah dihasilkan dengan menggunakan program SPSS maka kita lihat pada bagian akhir terdapat keterangan mengenai stem width : 10000. Hal ini dapat diartikan bahwa setiap angka yang terdapat di dalam sistem merupakan bilangan puluhan ribu. Dengan demikian, ketika kita menemukan angka 5, maka angka tersebut berarti 50000.
Selanjutnya, terdapat pula keterangan each cases : 8 cases, hal ini menunjukkan bahwa setiap angka yang terdapat didalam leaf, sebenarnya mewakili 8 data.
MODUL 3
UKURAN PEMUSATAN DAN UKURAN PENYEBARAN
Dalam modul ini kita akan mempelajari cara lain menyajikan data selain dengan menggunakan tabel frekuensi maupun dengan menggunakan grafik atau diagram. Dalam modul ini kita akan mempelajari cara lain menyajikan data. Data yang akan kita hitung dengan menggunakan ukuran pemusatan dan ukuran penyebaran. Ukuran pemusatan akan membantu kita untuk mengetahui bagaimana kecendrungan data yang ada. Data akan memusat di titik mana. Demikian pula dengan ukuran penyebaran akan membantu kita dalam mengetahui seberapa jauh penyebaran data yang ada atau dengan kata lain seberapa banyak variasi dari data yang ada.
Dengan mempelajari ukuran pemusatan dan ukuran penyebaran kita akan mengetahui lebih cepat dibanding dengan melihat tabel frekuensi maupun grafik. Dalam hal ini, ukuran pemusatan yang akan kita bahas antara lain nilai rata-rata, nilai modus, dan nilai median. Sedangkan untuk ukuran penyebaran akan kita bahas mengenai range, standar deviasi, dan standar variansi. Sebenarnya masih ada ukuran pemusatan dan ukuran penyebaran selain keenam yang sudah kita sebutkan, namun yang paling banyak digunakan adalah keenam pengukuran tersebut.
Seperti halnya ketika kita membahas tentang penyajian data dengan menggunakan tabel frekuensi dan grafik maka penggunaan ukuran pemusatan dan ukuran penyebaran juga terkait dengan skala pengukuran yang sudah kita bahas dalam modul satu. Ada ukuran pemusatan yang hanya bisa diaplikasikan dalam skala tertentu, demikian pula dengan ukuran penyebaran.
Dengan demikian, jika anda masih belum memahami materi tentang skala, ada baiknya anda kembali memeplajari materi tersebut sehingga akan mempermudah dalam memahami tentang ukuran pemusatan dan ukuran penyebaran.
KB 1 : UKURAN PEMUSATAN
Ukuran pemusatan bisa diartikan sebagai nilai tunggal yang mewakili suatu kumpulan data. Nilai tersebut akan menunjukkan pusat nilai data. Seperti sudah disinggung, bahwa setiap kumpulan data tentunya akan memiliki kecendrungan untuk mengumpul pada titik tertentu. Titik dimana kumpulan data itu memusat dinamakan dengan titik pusat.
Dengan demikian, titik pusat itulah yang akan mewakili keseluruhan data yang ada. Sebagai contoh, dalam suatu kelas terdapat 50 mahasiswa. Dari ke 50 mahasiswa itu, mereka tentunya ada yang memiliki usia yang sama, dan ada yang memiliki usia yang berbeda. Nah untuk mempermudah dalam penyampaian berita, kita tidak mungkin menyebut satu persatu usia dari ke 50 mahasiswa yang ada, namun kita dapat mengambil satu nilai yang dianggap mewakili ke 50 mahasiswa tersebut. Nilai yang akan kita mabil inilah yang nantinya akan kita sebut dengan ukuran pemusatan.
Seperti juga sudah disinggung dalam pendahuluan, dalam kegiatan belajar satu ini, kita akan membahas mengenai nilai rata-rata, nilai modus, dan nilai median. Kita juga sudah tahu bahwa penggunaan masing-masing nilai dipengaruhi oleh skala pengukuran. Untuk itu, kita akan melihat ukuran pemusatan yang bisa digunakan terkait dengan skala pengukuran yang tergambar dalam tabel berikut :
Tabel 3.1
| Skala Pengukuran |
Nilai Pemusatan |
| Modus |
Median |
Mean |
| Nominal |
v |
|
|
| Ordinal |
v |
v |
|
| Interval |
v |
v |
v |
| Rasio |
v |
v |
v |
Tabel 3.1 memberikan gambaran bahwa nilai pemusatan modus, dapat digunakan baik didalam skala pengukuran nominal, ordinal, interval, maupun rasio. Nilai pemusatan median tidak bisa digunakan untuk variabel yang berskala nominal, dan nilai pemusatan mean (rata-rata) tidak dapat digunakan untuk variabel dengan skala nominal dan ordinal. Untuk lebih jelasnya, kita akan bahas lebioh lanjut mengenai nilai pemusatan yang ada.
A. MODUS
Merupakan nilai pengamatan yang paling sering muncul. Dalam sebuah distribusi data, bisa saja distribusi tersebut memiliki satu nilai modus, beberapa nilai modus, atau justru tidak memiliki nilai modus.
Contoh sebuah distribusi data dengan satu nilai modus; nilai ujian akhir pengantar statistik sosial dari 20 mahasiswa yang ikut ujian adalah sebagai berikut :
| 50 |
78 |
65 |
82 |
71 |
50 |
70 |
60 |
88 |
90 |
| 72 |
63 |
50 |
66 |
77 |
50 |
62 |
71 |
60 |
55 |
Dari distribusi data tersebut, maka kita dapat simpulkan bahwa nilai pengamatan yang paling sering muncul adalah 50 (muncul sebanyak 4 kali) sehingga distribusi data tersebut memiliki satu nilai modus yaitu 50.
Contoh sebuah distribusi data dengan beberapa nilai modus; nilai ujian akhir pengantar statistik sosial dari 20 mahasiswa yang ikut ujian adalah sebagai berikut :
| 50 |
78 |
65 |
82 |
71 |
50 |
70 |
60 |
88 |
90 |
| 72 |
60 |
50 |
66 |
77 |
50 |
62 |
71 |
60 |
55 |
Dari distribusi data tersebut, maka kita dapat simpulkan bahwa nilai pengamatan yang paling sering muncul adalah 50 (muncul sebanyak 4 kali) dan 60 (muncul sebanyak 4 kali) sehingga distribusi data tersebut memiliki dua nilai modus, yaitu 50 dan 60.
Untuk distribusi data yang memiliki 2 nilai modus kita sebut dengan bimodus. Untuk distribusi data yang memiliki tiga nilai modus, kita sebut trimodus. Sedangkan suatu distribusi data yang memiliki lebih dari tiga nilai modus kita sebut multimodus.
Contoh sebuah distribusi data yang tidak memiliki nilai modus; nilai ujian akhir pengantar statistik sosial dari 20 mahasiswa yang ikut ujian adalah sebagai berikut :
| 52 |
78 |
65 |
82 |
79 |
53 |
70 |
69 |
88 |
60 |
| 72 |
66 |
75 |
64 |
77 |
58 |
62 |
71 |
61 |
55 |
Dari distribusi data tersebut, maka kita bisa simpulkan bahwa tidak ada nilai pengamatan yang muncul lebih sering dibanding data lain sehingga kita bisa katakan bahwa distribusi tersebut tidak memiliki nilai modus.
Karakteristik Nilai Modus adalah :
1. dapat digunakan untuk data kualitatif dan kuantitatif
2. dapat memiliki lebih dari satu nilai atau tidak sama sekali
3. dapat digunakan untuk skala nominal, ordinal, interval dan rasio
4. tidak dipengaruhi oleh nilai ekstrem
Pengertian dari nilai ektrem adalah nilai yang menyimpang terlalu jauh dari data lainnya dalam sebuah distribusi. Contoh : hasil pengumpulan data terhadap 7 orang adalah sebagai berikut :
50 50 50 60 60 65 100
Nilai pengamatan 100 adalah nilai ekstrem karena nilai lainnya berkisar dalam rentang yang tidak jauh (50 - 65), namun demikian nilai pengamatan ini tidak berpengaruh pada nilai modus (dalam distribusi ini modusnya adalah 50).
1. Modus untuk Data Kualitatif
Menghitung modus untuk data kualitatif dilakukan dengan cara melihat jumlah pengamatan terbanyak. Contoh modus untuk data kualitatif.
Tabel 3.2
Lokasi Tempat Tinggal
| Lokasi |
Frekuensi |
Persentase |
| Bali |
15 |
15 |
| Jawa |
30 |
30 |
| Sumatera |
15 |
15 |
| Kalimantan |
20 |
20 |
| Sulawesi |
20 |
20 |
| Total |
100 |
100 |
Tabel 3.2 menunjukkan bahwa nilai modus berada di Jawa (30%) sehingga bisa kita simpulkan bahwa sebagian besar mahasiswa tingga di Pulau Jawa.
2. Modus untuk Data Kuantitatif
Untuk menghitung modus pada data kuantitatif, kita perlu bedakan antara data kuantitatif yang tidak dikelompokkan dan data kuantitatif yang dikelompokkan.
a. Modus untuk data kuantitatif yang tidak dikelompokkan
Menghitung modus untuk data kuantitatif yang tidak dikelompokkan sama dengan menghitung modus untuk data kualitatif. Kita tinggal melihat nilai yang paling sering muncul. Kita ambil contoh yang sudah ada dalam penjelasan sebelumnya.
Nilai modus untuk distribusi data ini adalah 50 (muncul 3 kali).
b. Modus untuk data kuantitatif yang dikelompokkan
Menghitung modus untuk data kuantitatif yang dikelompokkan dilakukan dengan menggunakan rumus. Tumus untuk menghitung nilai modus adalah sebagai berikut :
Keterangan :
B1 = batas bawah kelas nyata untuk kelas yang mengandung modus
d1 = selisih frekuensi antara kelas yang mengandung modus dengan frekuensi kelas sebelumnya
d2 = selisih frekuensi antara kelas yang mengandung modus dengan frekuensi kelas sesudahnya
i = interval kelas
Kita coba terapkan rumus tersebut untuk melihat nilai modus pada tabel berikut.
Tabel 3.3 menunjukkkan pada kita bahwa kelas yang mengandung modus adalah kelas dengan batas nyata 68,5
< x
< 77,5 (sebanyak 19 nilai pengamatan). Dengan demikian, kita dapat masukkan data tersebut ke dalam rumus :
Dengan demikian, nilai modus untuk Tabel 3.3 adalah 74,8. Satu hal yang harus kita perhatikan adalah nilai modus, harus masuk ke dalam rentang kelas yang menunjukkan pengamatan terbanyak (dalam Tabel 3.3 adalah 68,5 < x < 77,5) sehingga 74,8 memang masuk ke dalam rentang nilai kelas tersebut.
Untuk distribusi data yang mengandung lebih dari satu nilai modus maka rumus yang ada harus dihitung sesuai dengan banyaknya nilai modus yang ada.
B. MEDIAN
Median adalah titik tengah dari semua nilai setelah diurutkan dari nilai terkecil hingga nilai terbesar atau sebaliknya. Dengan demikian, akan terdapat sejumlah nilai pengamatan yang sama, baik di bawah nilai tengah maupun di atas nilai tengah. Dengan kata lain, median membagi seluruh nilai pengamatan dengan komposisi 50% data di bawah nilai tengah dan 50% data di atas nilai tengah.
Karakteristik nilai median adalah :
1. bisa digunakan untuk data kualitatif dan data kuantitatif
2. satu distribusi data hanya memiliki satu nilai
3. bisa digunakan untuk skala ordinal, interval, dan rasio
4. tidak dipengaruhi oleh nilai ekstrem.
1. Median untuk Data Kualitatif
Menghitung median untuk data kualitatif dilakukan dengan cara melihat nilai kumulatif dari frekuensi atau persentase. Contoh; median untuk data kualitatif :
Frekuensi kumulatif didapatkan dengan menjumlah frekuensi kelas yang dihitung dengan kumulasi kelas sebelumnya. Jadi perhitungannya sebagai berikut :
Tabel 3.4 menunjukkan bahwa nilai median berada di SMP sehingga bisa kita simpulkan bahwa 50% warga memiliki pendidikan SD sampai SMP, sedangkan 50% lainnya memiliki pendidikan SMA dan PT.
2. Median untuk Data Kuantitatif
Seperti halnya dalam menghitung nilai modus maka menghitung median untuk data kumulatif perlu dibedakan ke dalam data yang tidak dikelompokkan dan data yang dikelompokkan. Untuk itu kita akan lihat satu persatu.
a. Median untuk data kuantitatif yang tidak dikelompokkan.
Untuk menghitung median pada data yang tidak dikelompokkan maka kita harus menghitung tahapan sebagai berikut :
1) Mengurutkan nilai pengamatan, mulai dari yang terkecil sampai yang terbesar atau sebaliknya.
2) Menentukan posisi median dengan rumus
dimana n = banyaknya data yang diobservasi
3) Mencari Nilai Median. Satu hal yang harus diingat adalah nilai mediannya adalah data yang berada pada posisi mediannya.
Kita coba lihat dengan contoh data yang sudah kita miliki pada saat membahas modus.
Langkah pertama, data ini kita urutkan dari yang terkecil menjadi sebagai berikut :
Langkah kedua, menentukan posisi median sehingga
Langkah ketiga, mencari nilai median. 10,5 diartikan sebagai data yang berada posisi 10 dan 11 sehingga data yang ada pada posisi 10 dan 11 harus kita bagi lagi menjadi 2, dengan demikian nilai mediannya adalah
b, Median untuk data kuantitatif yang dikelompokkan
Untuk menghitung nilai median bagi data kuantitatif yang dikelompokkan digunakan rumus sebagai berikut :
Keterangan :
B1 = batas bawah kelas nyata untuk kelas yang mengandung modus
n = banyaknya data
Cfb = frekuensi kumulatif kelas yang berada di bawah kelas yang mengandung median
fMd = frekuensi kelas yang mengandung media
i = interval kelas
Kita coba terapkan rumus tersebut untuk melihat nilai median pad tabel berikut :
Tabel 3.5 menunjukkan pad kita bahwa kelas yang mengandung median adalah kelas dengan batas nyata 68,5 < x < 77,5 (Hal ini terjadi karena jumlah data seluruhnya 80 sehingga posisi median berada di data pengamatan 40 dan 41 atau 40,5). Dengan demikian, kita bisa masukkan data tersebut ke dalam rumus :
Dengan demikian, nilai median untuk tabel 3.5 adalah 75,6. Seperti halnya yang berlaku dalam perhitungan modus maka nilai median harus masuk ke dalam rentang kelas yang mengandung median, yaitu 68,5 < x < 77,5
C. RATA-RATA (MEAN)
Menu adalah nilai rata-rata dari seluruh data yang ada dalam sebuah distribusi data. Nilai rata-rata dianggap sebagai perwakilan seluruh data yang ada. Dengan demikian, untuk menghitung nilai rata-rata didapat dengan cara menjumlahkkan seluruh data yang ada, lalu dibagi dengan jumlah data yang ada.
Karakteristik nilai mean adalah :
1. hanya bisa digunakan untuk data kuantitatif saja
2. satu distribusi data hanya memiliki satu nilai
3. hanya bisa digunakan untuk skala interval/rasio
4. dipengaruhi oleh nilai ekstrem
Pengaruh nilai ekstrem dalam sebuah distribusi data sangat kuat terhadap nilai mean karena perhitungan didasarkan pada penjumlahan seluruh data yang ada. Kita coba bandingkan 2 distribusi data yang hampir serupa, namun tidak sama karena adanya nilai ekstrem.
Distribusi 1, terdiri dari kumpulan data 10, 20, 30, 40, 50 maka nilai rata-ratanya adalah (10 + 20 + 30 + 40 + 50) / 5 = 30
Bandingkan dengan distribusi 2, yang terdiri dari kumpulan data 10, 20, 30, 40, 150 maka nilai rata-ratanya adalah (10 + 20 + 30 + 40 + 150) / 5 = 50
Dengan demikian, adanya nilai ekstrem pada distribusi 2, membuat nilai rata-rata menjadi menyimpang jauh dari keseluruhan data yang ada dalam distribusi data.
Untuk menghitung nilai rata-rata, kita juga perlu membedakan antara data yang dikelompokkan dan data yang tidak dikelompokkan dan juga perlu dibedakan anytara data yang ada di populasi dan data yang ada di tingkat sampel. Kita akan lihat satu persatu.
1. Mean untuk Data yang Tidak Dikelompokkan.
Untuk data yang tidak dikelompokkan, kita akan langsung membedakan antara data yang ada di populasi dan data yang ada di tingkat sampel, dengan menggunakan rumus sebagai berikut :
Kita langsung coba terapkan rumus mean ke dalam contoh berikut.
Nilai ujian akhir pengantar statistik sosial dari 20 mahasiswa yang ikut ujian adalah sebagai berikut :
2. Mean untuk Data yang DikelompokkanSeperti halnya untuk data yang tidak dikelompokkan, dalam perhitungan mean untuk data yang dikelompokkan, kita juga akan langsung membedakan antara data yang ada di populasi dan data yang ada di tingkat sampel, dengan menggunakan rumus sebagai berikut :
Kita langsung coba terapkan rumus mean ke dalam contoh berikut :
Jadi nilai rata-rata untuk Tabel 3.6 adalah :
KB 2 : UKURAN PENYEBARAN
Ukuran penyebaran, merupakan ukuran yang memberikan gambaran kepada kita mengenai variasi dari data yang ada dalam sebuah distribusi. Jika ukuran pemusatan menunjukkan bagaimana data yang ada memusat pada satu titik maka ukuran penyebaranmenunjukkan seberapa banyak dan seberapa jauh data yang ada menyebar. Beberapa distribusi data, bisa saja memiliki ukuran pemusatan yang sama, namun setiap distribusi data memiliki variasi data yang berbeda-beda. Kita coba lihat ilustrasi berikut ini :
Ketiga distribusi yang ada menunjukkan kesamaan ukuran pemusatan, yaitu rata-ratanya 21, namun demikian jika kita cermati variasi data yang ada maka menunjukkan adanya perbedaan antara distribusi data 1, 2, dan 3. Dengan demikian, dalam penyajian data, tidak cukup hanya menampilkan ukuran pemusatan saja, namun ukuran penyebaran juga perlu kita tampilkan.
Ukuran penyebaran akan memberikan gambaran kepada kita tentang seberapa jauh data yang ada menyimpang dari nilai pusatnya. Semaki besar nilai yang ditunjukkan ukuran penyebaran, semakin menyimpang data dari titik pusatnya sehingga data yang seperti ini, menunjukkan adanya heterogenitas data, sedangkan semakin kecil nilai yang ditunjukkan ukuran penyebaran maka data yang ada semakin terpusat sehingga data yang seperti ini, akan menunjukkan adanya homogenitas data. Kita akan membahas tentang Index of qualitative variation (IQV) jangkauan/rentang (range), simpangan baku/deviasi standar, dan variasi.
A. INDEX QUALITATIVE VARIATION (IQV)
IQV merupakan ukuran penyebaran yang digunakan di dalam data kualitatif. Perhitungan nilai IQV berbentuk persentase, dimana nilai IQV 100% menunjukkan adanya heterogenitas yang mutlak, sedangkan nilai IQV 0% menunjukkan adanya homogenitas yang mutlak. Untuk menghitung IQV kita gunakan rumus sebagai berikut :
l = jumlah kategori
n = jumlah data
Kita langsung saja dengan menggunakan contoh kasus berikut :
Dari hasil perhitungan iqv, kita bisa simpulkan bahwa data mengenai alasan pemilihan perguruan tinggi sangat heterogen (mendekati 100%).
B. JANGKAUAN (RANGE)
Jangkauan atau jarak merupakan ukuran penyebaran yang palig sederhana untuk menghitung dan menginterpretasikan data. Rentang bisa kita artikan sebagai perbedaan antara nilai terbesar dan nilai terkecil dalam sebuah distribusi data.
Mengingat rentang merupakan ukuran penyebaran yang paling sederhana maka perhitungan ini memang jarang sekali digunakan. Selain karena merupakan perhitungan sederhana, alasan lainnya karena nilai ini juga sangat dipengaruhi oleh nilai ekstrem. Contoh perhitungan rentang bisa kita lihat dengan menggunakan distribusi data sebagai berikut :
Nilai ujian akhir pengantar statistik sosial dari 20 mahasiswa yang ikut ujian adalah sebagai berikut :
Rentang yang ada dalam ujian mahasiswa adalah : 40. Angka ini didapat dari selisih antara nilai tertinggi (90) dengan nilai terendah (50).
C. VARIANSI DAN DEVIASI STANDAR
Variansi dan deviasi standar merupakan ukuran penyebaran yang didasarkan pada penyimpangan setiap nilai pengamatan terhadap nilai rata-rata. Variansi merupakan jumlah kuadrat dari selisih nilai pengamatan dengan nilai rata-rata hitung,sedangkan deviasi standar merupakan akar dari variansi. Dalam menghjitung variansi mauoun deviasi standar, kita harus membedakan antara data yang dikelompokkan dan data yang tidak dikelompokkan dan juga antara populasi dan sampel.
1. Variansi dan Deviasi Standar untuk Data yang tidak Dikelompokkan
Rumus untuk menghitung variansi (untuk populasi dan sampel) dari data yang tidak dikelompokkan adalah sebagai berikut :
Kita akan coba langsung dengan menerapkan kasus yang ada dengan menggunakan distribusi data yang sudah kita miliki sebelumnya.
Nilai ujian akhir pengantar statistik sosial dari 20 mahasiswa yang ikut ujian adalah sebagai berikut :
Untuk menghitung nilai variansi dan deviasi standar, langkah pertama adalah menghitung nilai rata-ratanya terlebih dahulu. Nilai rata-rata untuk distribusi data yang ada adalah :
Setelah kita ketahui nilai rata-ratanya maka ada baiknya kita membuat tabel sebagai berikut :
Dengan demikian, nilai variansi jika data tersebut merupakan data populasi adalah :
Nilai variansi jika data tersebut merupakan data sampel adalah :
Jika kita sudah mengetahu nilai variansi maka untuk menghitung nilai deviasi standar, kita tinggal menghitung akar dari variansi sehingga deviasi
2. Variansi dan Deviasi Standar untuk Data yang Dikelompokkan
Rumus untuk menghitung variansi (untuk populasi dan sampel) dari data yang tidak dikelompokkan adalah sebagai berikut :
Kita langsung saja dengan contoh menggunakan kasus yang sudah kita miliki :
Untuk menghitung nilai variansi dan deviasi standar, langkah pertama adalah menghitung nilai rata-ratanya terlebih dahulu. Nilai rata-rata untuk distribusi data yang ada adalah :
setelah kita ketahui nilai rata-ratanya maka ada baiknya kita membuat tabel sebagai berikut :
MODUL 4 :
PROBABILITA
Dalam setiap penelitian, peneliti ingin mengambil suatu kesimpulan atas apa yang telah diteliti. Misalnya, peneliti melakukan penelitian mengenai sikap mahasiswa UT terhadap pelayanan mahasiswa (Pelma). Untuk mengetahui bagaimana sikap mahasiswa UT tentunya akan sulit jika peneliti meneliti seluruh mahasiswa UT yang berjumlah ratusan ibu, dan tersebar di seluruh pulau yang ada di Indonesia. Satu cara yang bisa dilakukan adalah dengan cara mengambil sampel. Misalnya, peneliti mengambil sebanyak sepuluh ribu mahasiswa. Sepuluh ribu mahasiswa tersebut, kita sebut sebagai sampel. Nah, setelah meneliti sepuluh ribu mahasiswa tersebut maka peneliti dapat mengambil kesimpulan atas sikap mahasiswa yang diteliti atau dengan kata lain peneliti dapat mengambil kesimpulan atas sampel yang diambil. Anggaplah sikap dari sepuluh ribu mahasiswa yang dijadikan sampel adalah positif.
Apakah penelitian tu sudah selesai? Bukankah penelitian sesungguhnya ingin mengetahui bagaimana sikap mahasiswa secara kesluruhan? Untuk itu, peneliti bisa melakukan suiatu teknik yang kita sebut sebagai inferensi ; yaitu penarikan kesimpulan terhadap data populasi yang didasarkan pada data yang ada di sampel.
Utuk dapat melakukan inferensi maka syarat utama yang harus dipenuhi adalah pengambilan sampel yang representatif atau mewakili. Sampel dikatakan dapat mewakili populasi, apabila proses penarikannya dilakukan secara probabilitas. Apa pengertian probabilitas dan bagimana akurasi dalam inferensi inilah yang akan kita pelajari.
KB 1 : TEORI PROBABILITA
A. PENGERTIAN PROBABILITA
Apa sesungguhnya pengertian dari probabilita? Pada dasrnya dalam kehidupan sehari-hari kita selalu melakukan perhitungan-perhitungan probabilita. Pernakah anda memperhitungkan siapa yang akan menang dalam pertandingan final sepak bola antara Inggris melawan Belanda? Atau pernakah anda bertanya apakah saya akan lulus dalam ujian statistik? Nah jawaban dari masing-masing pertanyaan tadi sederhana. Bisa saja, Belanda memenangkan pertandingan melawan Inggris. Kemungkinan lain, bisa saja Inggris memenangkan pertandingan. Demikian halnya, bisa saja Anda lulus dalam ujian statistik, atau bisa juga anda tidak lulus dalam ujian statistik.
Apabila kita perhatikan dengan seksama maka jawaban yang ada merupakan jawaban yang tidak pasti, bisa Belanda yang menang, bisa Inggris yang menang, bisa lulus atau bisa tidak lulus. Dalam kedua kasus ini. sesungguhnya kita sudah melakukan teknik probabilitas. Dengan demikian, probabilitas dapat kita artikan sebagai suatu perhitungan yang didasarkan pada peluang dan kemungkinan.
Berdasarkan kasus tadi, kita juga dapat mengetahui bagaimana peluang dari satu kejadian. Peluang Belanda untuk memenangkan pertandingan adalah 0,5. Demikian pula peluang Inggris utnuk memenangkan pertandingan juga 0,5. Bagaimana kita dapat mengatakan demikian? Dalam hal ini, kita perlu memperhatikan apa yang disebut sebagai alternatif kemungkinan (dalam statistik diberi notasi n), dan kita juga harus tahu peristiwa atau kejadian atau percobaan yang dilakukan (diberi notasi x). Dengan demikian, ada 2 tim yang masing-masing memiliki 2 kemungkinan (alternatif kemungkinan menang atau kalah), dan ada satu peristiwa (yang diinginkan adalah menang) sehingga berdasar rumus probabilitas maka kemungkinan Belanda menang adalah satu dari dua kemungkinan atau 1/2 (0,5%).
Demikian pula kemungkinan lulus ujian, dimana ada 2 alternatif kemungkinan (lulus atau gagal), dan ada satu peristiwa yang diinginkan, yaitu lulus (jika lulus tentunya tidak mungkin gagal). Dengan demikian, probabilita anda lulus ujian adalah satu dari dua kemungkinan atau 1/2 (0,5).
Nilai peluang atau probabilita, berkisar antara 0 hingga 1. Peluang nol adalah peluang terhadap suatu kejadian yang tidak mungkin terjadi. Peluang bahwa manusia bisa hidup dengan tidak bernapas selama 24 jam adalah nol (tidak mungkin terjadi). Peluang 1 adalah peluang terhadap suatu kejadian yang pasti terjadi. Peluang bahwa manusia perlu udara untuk hidup adalah satu (pasti terjadi), sedangkan peluang yang terjadi antara nol hingga satu adalah peluang yang banyak terjadi dalam kehidupan sosial manusia, seperti halnya kasus sepak bola.
Mari kita lihat contoh lain. Kita bermain-main dengan uang logam. Kita lemparkan uang logam ke udara, kemudian kita minta rekan kita menebak apakah sisi bagian atas berupa gambart atau angka. Berapa peluang munculnya gambar pada sisi bagian atas ketika uang logam sudah kita lempar? Ada dua sisi mata uang logam, suatu sisi berupa gambar dan satu sisi berupa angka. Dengan demikian,kemungkinan munculnya sisi gambar dalam lemparan adalah satu dari 2 kemungkinan.
Kemungkinan muncul gambar = peristiwa
Kemungkinan muncul angka = peristiwa
Keseluruhan peristiwa = ruang sampel = alternatif kemungkinan yang ada.
Untuk memahami tentang probabilita, kita sebaiknya mengetahui terlebih dahulu beberapa asumsi yang dijadikan dasar dalam teori probabilita sebagai berikut :
1. Probabilita akan berada pada nilai antara 0 sampai 1
2. Nilai peluang komplemen dari satu kejadian adalah 1 dikurangi nilai kejadian tersebut. Misalnya, peluang terjadinya kebakaran adalah 0,3 maka peluang tidak terjadinya kebakaran adalah 0,7.
3. P ( A ∪ B ) = P (A) + P (B) - P (A ∩ B). Notasi ∪ kita bahaskan sebagai "atau", sedangkan notasi ∩ kita bahaskan sebagai "dan".
Asumsi ini disebut juga non-exclusive (tidak saling terpisah), yaitu suatu kejadian di mana ada dua tau lebih kejadian yang dapat terjadi bersamaan, tetapi tidak selalu. Dengan kata lain, ada elemen bersama, yaitu ada elemen di A dan juga di B. Dalam Diagram Venn, terlihat bahwa ada kelompok A, Kelompok B, dan ada kelompok AB.
Rumus P ( A ∪ B ) = P (A) + P (B) - P (A ∩ B)
Contoh :
Apabila dalam satu kelas terdapat 50 orang mahasiswa, 35 diantaranya mengambil mata kuliah statistik, dan 35 lainnya mengambil mata kuliah metode penelitian. 20 dari mereka mengambil mata kuliah statistik dan metode penelitian. Pertanyaannya adalah berapa peluang mereka yang mengambil statistik saja atau metode penelitian saja? Apabila mereka yang mengambil statistik kita anggap kelompok A, dan mereka yang mengambil metode penelitian kelompok B. maka :
P (A) = 35/50 , P (B) = 35/50 , dan P (A ∩ B) = 20/50, maka
P ( A ∪ B ) = 35/50 + 35/50 - 20/50 = 1
Jika digambarkan dalam Diagram Ven akan tampak sebagai berikut :
Selain terdapat 3 asumsi dasar, dalam perhitungan probabilita juga ada 3 pendektan yang bisa digunakan sebagai berikut.
1. Pendekatan Klasik :
rumus yang digunakan adalah P (A) = x/n
dimana x = peristiwa dan n = ruang sampel
Contoh :
Kita memiliki sebuah dadu. Kita tahu bahwa dadu memiliki enam sisi, di mana setiap sisi memiliki satu bulatan hingga enam bulatan. Apabila kita melempar dadu tersebut maka berapa peluang munculnya sisi satu bulatan di atas? Berdasar rumus kita bisa hitung bahwa probabilita munculnya satu bulatan adalah 1/6
2. Pendekatan Frekuensi Relatif :
Untuk menghitung probabilita atas suatu kejadian kita memakai data masa lalu. Dengan demikian, pendekatan ini bisa digunakan apabila pengamatan dilakukan dari percobaan berulang, serta kondisi untuk jangka panjang relatif stabil.
Contoh :
Apabila diketahui data untuk tahun 1999 terjadi kecelakaan sebanyak 150 di mana 75 diantaranya karena supir mengantuk. Jika pada tahun 2000 terjadi 200 kecelakaan maka berdasar data yang ada pada tahun 1999 tersebut, kita bisa menduga bahwa tahun 2000 akan terjadi kecelakaan yang disebabkan mengantuk sebesar 7/150 x 200 = 100
3. Pendektan Subjektif :
Perhitungan probabilita ini didasarkan pada tingkat kepercayaan seseorang terhadap suatu kejadian. Orang-orang yang memiliki probabilita 0, sering kali kita sebut sebagai orang yang pesimis, sedangkan orang yang memiliki probabilita 1, kita sebut sebagai seorang yang optimis. Misalnya saja, saya ditanya apakah pemerintah Orba masih memiliki pengaruh di masa reformasi, saya bisa mengatakan kemungkinan itu kecil, hanya 10%. Dugaan ini didasarkan pada subjektivitas saja. Mungkin saja, organisasi nonpemerintah yang ada di luar pemerintah optimis (100%) bahwa pemerintah Orba masih memiliki pengaruh di masa reformasi.
B. ASAS-ASAS PERISTIWA
Dalam perhitungan probabilita ada beberapa peristiwa yang mungkin saja terjadi. Berikut ini akan kita lihat 4 asas peristiwa.
1. Mutually exclusive (saling terpisah);
Suatu peristiwa di mana ada dua atau lebih kejadian yang terpisah. Kejadian A terpisah dengan kejadian B. Dengan kata lain, tidak ada hubungan dari keterkaitan antara A dan B. Tidak ada elemen bersama, yaitu elemen yang ada di A dan sekaligus ada di B. Dalam Diagram Venn maka peristiwa ini dapat digambarkan sebagai berikut :
Rumus P ( A ∪ B ) = P (A) + P (B)
Rumus ini dibahasakan sebagai probabilita A atau B sama dengan probabilita A ditambah probabilita B.
Contoh :
Suatu instansi sedang mencari pegawai baru. Setelah diumumkan melalui surat kabar, ternyata ada 5 orang yang mengajukan lamaran kerja, yaitu Anto, Budi, Chyntia, Dedi, serta Eko. Pertanyaannya adalah berapa peluang bahwa yang terpilih atau pelamar yang diterima kerja di instansi tersebut adalah Anto atau Budi?
Probabilita atau peluang bahwa Anto terpilih adalah satu dari lima kemungkinan, demikian pula peluang bahwa Budi yang terpilih adalah satu dari lima kemungkinan, dengan demikian :
P ( A ∪ B ) = P (A) + P (B) = 1/5 + 1/5 = 2/5
2. Asas Peristiwa kedua adalah Peristiwa Independen (bebas);
Yaitu suatu peristiwa yang tidak memeperngaruhi peristiwa lainnya. Apabila kita melempar mata uang satu kali maka peluang munculnya gambar adalah 1/2.
Apabila kita melempar mata uang untuk kedua kalinya maka peluang munculnya gambar lagi adalah setengah. Hal ini terjadi karena kedua kejadian tersebut adalah independen, dimana lemparan pertama tidak mempengaruhi lemparan kedua. Kemudian, berapa peluang sisi gambar akan muncul dalam dua kali lemparan? Untuk menghitung peluang tersebut, kita dapat mengalikan hasil peluang marginal. Dengan demikian, rumus untuk kejadian gabungan independen adalah :
P (A ∩ B) = P(A) x P(B) sehingga peluang munculnya gambar pada putaran pertama dan gambar lagi pada putaran kedua adalah 1/2 x 1/2 = 1/4.
3. Asas Peristiwa yang ketiga adalah Asas Peristiwa Dependen;
Yaitu suatu peristiwa tergantung pada peristiwa lain. Kejadian ini juga sering disebut kejadian bersyarat, yaitu suatu peristiwa yang keberadaannya disyaratkan oleh peristiwa lain. Rumus untuk bersyarat yang dependen :
P(G/H) = P (GnH)
P(H)
P(G/H) dibahaskan sebagai peluang G jika H
Dengan demikian, apa yang menjadi syaratnya merupakan bilangan pembaginya. Misalnya, kita memasukkan 10 bola ke dalam sebuah wadah yang kosong dan tertutup, di mana ada 1 bola dengan warna hitam dan memiliki motif kotak. Pertanyaannya adalah berpa peluang terambilnya bola bermotif koyak jika bola tersebut berwarna hitam? Kita lihat satu persatu :
Peluang bola bermotif kotak dan berwarna hitam adalah 1/10
Peluang bola berwarna hitam adalah 4/10
Maka berdasar rumus bersyarat dependen peluang terambilnya bola bermotif kotak jika bola tersebut berwarna hitam adalah : 1 / 10 : 4 / 10 = 1/4
Saudara Mahasiswa, Anda telah mempelajari mengenai asas peristiwa, kini cobalah kerjakan tugas berikut, untuk membantu anda memahami materi yang ada. Cobalah mengerjakan sendiri, kemudian cocokkan dengan jawaban yang ada di bawah tugas ini.
Dari data yang ada di biro kepegawaian, tercatat ada 100 orang yang bekerja di sebuah perusahaan pemasaran. Dari 100 orang tersebut, tercatat posisi manajer sebanyak 10 orang, diantaranya lulusan perguruan tinggi sebanyak 5 orang. Mereka yang dari perguruan tinggi sendiri tercatat ada 20 orang, dan diantaranya menjadi staf sebanyak 10 orang. Total staf yang ada sebanyak 60 orang , dan diantaranya 25 orang lulusan SMA. Sementara itu terdapat 15 orang lulusan SMA yang menjabat sebagai sekretaris. Lulusan akademi yang bekerja di tempat tersebut sebanyak 40 orang, diantaranya yang menjabat sebagai manajer sebanyak 5 orang.
Hitunglah peluang seseorang adalah :
a. manager
b. lulusan akademi
c. sekretaris dan dia lulusan akademi
d. lulusan akademi dan menjabat sebagai staf
e. staf jika ia lulusan perguruan tinggi
f. lulusan SMA jika ia menjabat sebagai sekretaris
g. lulusan akademi atau menjabat sebagai manajer
Untuk bisa mengerjakan tugas tersebut, kita harus membuatb tabel silang terlebih dahulu :
Maka peluang seseorang adalah :
a. Manager = 10/100
b. lulusan akademi = 40/100
c. sekretaris dan dia lulusan akademi = 10/100
d. lulusan akademi dan menjabat sebagai staf = 25/100
e. staf jika ia lulusan perguruan tinggi = 10/20
f. lulusan SMA jika ia menjabat sebagai sekretaris = 15/30
g. lulusan akademi atau menjabat sebagai manaer = 40/100 + 10/100 - 5/100 = 45/100
C. RUANG SAMPEL
Apabila dalam bagian sebelumnya kita dapat menghitung berapa probabilita dari satu kejadian atau percobaan, dengan menghitung peluang yang diharapkan dibandingkan dengan semua alternatif kejadian yang mungkin terjadi maka kita juga dapat menghitung berapa banyak alternatif kejadian yang mungkin terjadi, bila percobaan dilakukan beberapa kali. Alternatif dari seluruh kejadian dalam beberapa percobaan tersebut, dikenal sebagai ruang sampel.
Misalnya saja, kita memiliki sebuah dadu, kita tahu bahwa dadu memiliki enam sisi. Masing-masing sisi berisi 1 bulatan, 2 bulatan, 3 bulatan, 4 bulatan, 5 bulatan, dan 6 bulatan. Apabila dadu tersebut kita lempar dua kali maka berapa kombinasi yang mungkin terjadi dalam dua kali lemparan tersebut? Untuk mengetahui ini, kita buat diagram berikut :
Dengan melihat diagram kombinasi maka kita tahu bahwa ada 36 kombinasi yang mungkin terjadi. Permasalahannya sekarang adalah ada beberapa perhitungan yang bisa membuat perbedaan jumlah kombinasi yang ada, yaitu apabila kita memperhitungkan pemulihan dan memperhatikan urutan.
1. Dengan Pemulihan dan Dengan Urutan
Dalam kondisi ini, kita memperhatikan pemulihan dan memperhatikan urutannya. Memperhatikan pemuloihan berarti apabila pada lemparan pertama sisi satu yang muncul maka sisi kedua masih memungkinkan sisi satu untuk muncul kembali.
Dengan demikian, kemungkinan hasil percobaan (1,1) adalah mungkin saja terjadi, demikian pula dengan sisi (2,2), (3,3). Memperhatikan urutan, berarti apabila lemparan pertama adalah sisi satu, dan lemparan kedua sisi dua maka akan berbeda dengan lemparan pertama sisi dua, dan lemparan kedua sisi satu : (1.2) ≠ (2.1). Dengan demikian, seluruh kombinasi yang ada dalam diageram di atas merupakan ruang sampel.
Rumus untuk ruang sampel dengan pemulihan dan dengan urutan adalah Nⁿ, di mana N = jumlah sisi (populasi) dan n = jumlah percobaan (sampel). Dalam kasus dadu ini maka Nⁿ = 6² = 36.
2. Tanpa Pemulihan dan Tanpa UrutanKondisi ini menunjukkan bila pada lemparan pertama sisi satu muncul maka pada lemparan kedua, sisi satu tidak mungkin muncul kembali. Tanpa urutan menunjuk pada kenyataan bahwa kombinasi (1,2) = (2,1), dan (3,5) = (5,3) sehingga kita hanya bisa menggunakan salah satu saja. Dengan demikian, dalam diagram kombinasi ruang sampelnya adalah :
Rumus untuk ruang sampel, tanpa pemulihan dan tanpa urutan adalah :
di mana N = jumlah sisi (populasi), dan n = jumlah percobaan (sampel), Rumus ini dijabarkan menjadi :
N! dibaca (N faktorial) adalah bilangan tersebut dikalikan bilangan yang ada dibawahnya hingga bilangan satu. Dengan catatan 0! = 1
Dalam kasus dadu ini maka :
3. Dengan Pemulihan dan Tanpa Urutan
Dengan pemulihan dan tanpa urutan dalam diagram kombinasi ruang sampelnya adalah :
Rumus untuk ruang sampel dengan pemulihan dan tanpa urutan adalah :
Rumus untuk ruang sampel, tanpa pemulihan dan dengan urutan adalah :
N (
N - 1) ... (
N -
n + 1). Didefinisikan sebagai N dikali (
N - 1) sampai dengan (
N -
n + 1). Dalam kasus dadu maka hasilnya adalah : 6(6 - 1) ... (6 - 2 +1) --> 6.5 = 30
Dengan menggunakan rumus ruang sampel, kita bisa mengetahui berapa jumlah seluruh kombinasi yang ada. Namun, kita belum bisa mengetahui kombinasinya. Untuk kasus dadu yang dilempar dua kali, kita bisa mengetahui kombinasinyya dengan menggunakan tabel silang seperti yang sudah kita pelajari bersama, namun untuk jumlah sampel yang lebih dari dua maka kita bisa gunakan diagram pohon akar. Kita coba lihat dalam kasus berikut :
Iwan adalah salah satu dari panitia pemilihan kepemimpinan organisasi pemuda, mencatat terdapat 3 calon yang memenuhi kualifikasi untuk menjabat sebagai Ketua, Sekretaris Umum, dan Bendahara Umum, yaitu Bonansa, Satrio, dan Sundari. Iwan mencoba untuk menentukan posisi mereka masing-masing. Dengan menggunakan diagram pohon maka kombinasi yang mungkin terjadi adalah sebagai berikut :
Dari diagram pohon ini, kita bisa lihat bahwa terdapat 27 kombinasi yang muncul. Namun dalam kasus pemilihan ketua, sekretaris, dan bendahara maka pemulihan tidak dimungkinkan. Tidak mungkin Bonansa menjadi ketua sekaligus menjadi sekretaris. Sementara itu, urutan menjadi mungkin karena bisa saja dalam salah satu kombinasi Bonansa menjadi ketua, namun dalam kombinasi lain, Bonansa menjadi sekretaris. Dengan demikian, maka kombinasi yang pasti untuk kasus ini adalah :
KB 2 : DISTRIBUSI PELUANG
Akan dibahas mengenai peluang atau probabilita dari suatu kejadian. Dalam statistik kita juga mempelajari peluang dari suatu distribusi data. Apabila kita bicara mengenai distribusi peluang maka sama halnya dengan kita mempelajari distribusi frekuensi, yang sudah dipelajari sebelumnya.
Dengan demikian, distribusi peluang kita dapatkan dengan cara melakukan beberapa percobaan. Perbedaan antara distribusi peluang dan distribusi frekuensi adalah bila kita bicara mengenai distribusi frekuensi maka kita bicara mengenai data yang terjadi pada hasil percobaan (observed data), sedangkan dalam distribusi peluang, kita bicara mengenai data yang diharapkan atau di duga terjadi pada hasil percobaan (expected data). Berdasarkan hal tersebut, maka distribusi peluang sering kali disebut juga sebagai distribusi teoretis.
Kita coba ambil contoh tentang pelemparan mata uang logam. Uang logam memiliki 2 sisi, yaitu sisi angka dan sisi gambar. Jika kita melakukan percobaan dengan melempar uang logam itu dua kali maka kemungkinan munculnya sisi angka adalah sebagai berikut :
Dengan demikian, probabilita munculnya sisi angka sebanyak 1 kali adalah 0,5 probabilita muncyulnya sisi angka sebanyak 2 kali adalah 0,25 dan probabilita sisi angka tidak pernah muncul adalah 0,25
Jika kita membicarakan distribusi peluang, kita akan membahas mengenai 2 kategori data, yaitu data yang kontinu dan data diskret. Data diskret adalah data yang tidak mengandung pecahan (bilangan bulat) mislanya 1; 12; 101; 5000. Data kontoinu adalah data yang tidak bulat, dengan kata lain mengandung nilai pecahan misalnya 10,5; 10,7; 100,23.
A. DISTRIBUSI PROBABILITA DISKRET
Distribusi ini sesuai dengan namanya, hanya digunakan untuk variabel yang memiliki skala diskret, yaitu nilainya bulat dan tidak dapat dibuat pecahan. Misalnya, sikap seseorang, kelulusan seseorang, kesuksesan seseorang, dsb. Distribusi probabilita diskret dibedakan menjadi dua, yaitu distribusi binomial dan distribusi poisson.
1. Distribusi Binomial
Distribusi binomial adalah distribusi untuk variabel dengan dua kategori.
Distribusi binomial digunakan untuk data atau variabel diskret.
Distribusi binomial memiliki karakteristik sebagai berikut :
a. Mutually exclusive (tidak A maka pasti B)
b. Probabilita sukses; p
c. Probabilita gagal; 1 - q
d. Asas peristiwa; independen
Rumus :
n = jumlah percobaan
x = jumlah kemungkinan
p = jumlah peluang
q = jumlah kemungkinan gagal.
Misalnya saja, kepada mahasiswa diberikan kesempatan untuk tidak masuk kuliah sebanyak 4 kali dari 10 kali pertemuan. Jika dalam satu kelas ada 5 mahasiswa maka peluang kelima mahasiswa tersebut jika tidak ada yang tidak masuk?
==> p = 0,4(4/10) q = 0,691-0,4) n = 5 x = 0
Kita coba lihat contoh lain, misalnya berapa peluang kelima mahasiswa tersebut jika 1 yang tidak masuk?
==> p = 0,4 q = 0,691-0,4) n = 5 x = 0
Prinsip Pemakaian Tabel Binomial !
Selain dengan cara menghitung menggunakan rumus, kita juga bisa menemukan distribusi binomial dengan memakai tabel binomial. Kita coba kasus yang tadi sudah kita hitung, dimana diketahui n = 5, P = 0,4, x = 0
Perhatikan cuplikan tabel berikut ini. (Tabel yang lebih lengkap bisa Anda lihat di bagian lampiran).
maka dalam tabel binomial, titik yang ditunjuk adalah :
Nilai 0,0778 berdasarkan tabel adalah sama dengan nilai hasil perhitungan dengan rumus setelah adanya pembulatan.
Kita coba kasus yang kedua, dimana n = 5, P = 0,4, x = 1
Dengan demikian, penggunaan tabel akan mempermudah kita dalam menemukan nilai peluang distribusi binomial.
Satu hal yang perlu diingat, ada tabel distribusi binomial yang kumulatif, namun ada juga tabel yang tidak kumulatif, untuk itu anda harus memperhatikan judul tabel yang ada. Untuk tabel yang kumulatif maka harus dikurangi dengan nilai sebelumnya, sedangkan untuk tabel yang tidak kumulatif, angka yang tertera tidak perlu dikurangi dengan nilai sebelumnya. Dalam BMP ini, kita gunakan tabel yang tidak kumulatif sehingga kita tidak perlu mengurangi dengan nilai sebelumnya.
Beberapa catatan tentang distribusi binomial :
1. Dalam beberapa kasus tertentu, sering kali kita tidak mengetahui nilai rata-ratanya atau kita tidak mengetahui nilai standard deviasinya. Untuk mengatasi hal tersebut kita bisa memakai rumus berikut Rumus :
Mean (𝞵) : n.p
Simpangan baku (S) : npq
Misalnya saja, kita menduga bahwa dari seluruh peserta ujian, 80% mahasiswa akan lulus. Jika dari seluruh peserta diambil 10 mahasiswa maka kita bisa menghitung rata-ratanya : 10(0,8) = 8. Simpangan baku : 10(0,8)(0,2) = 1,265.
2. Dalam mempelajari distribusi binomial, ada satu ketentuan yang berlaku, bahwa distribusi binomial dipengaruhi niolai p. Apabila p = 0,5 maka distribusi binomial tersebut akan membentuk distribusi yang simetris, apabila nilai p semakin jauh dari 0,5 maka bentuk distribusi akan semakin menceng. Apabila p < 0,5 maka distribusi akan menceng ke kanan, sedangkan apabila p > 0,5 maka distribusi akan menceng ke kiri.
Saudara mahasiswa, Anda telah mempelajari mengenai distribusi probababilita binomial, kini cobalah kerjakan tugas berikut, untuk membantu anda memahami materi yang ada. Cobalah mengerjakan sendiri, kemudian cocokkan dengan jawaban yang ada di bawah ini.
Berdasarkan data yang dimiliki oleh Polda Metro Jaya, diketahui bahwa 60% pengemudi angkutan umum di Jakarta dan sekitarnya menggunakan sabuk pengaman ketikan mengemudikan kendaraan. Jika dipilih 10 pengemudi, hitunglah peluang :
- 7 pengemudi menggunakan sabuk pengaman
- 7 pengemudi atau kurang menggunakan sabuk pengaman
Gunakan rumus untuk mengerjakan soal pertama dan gunakan tabel binomial untuk mengerjakan soal kedua.
Soal pertama :
p = 0,6
N = 10
Soal Kedua :
Yang dicari adalah x < 7, maka kita bisa menghitung peluang dari 0 hingga 7, lalu kita jumlahkan atau kita bisa menghitung peluang 8 hingga 10, setelah selesai, kita kurangi 1 dengan jumlah yang sudah kita dapatkan. Cara ini lebih sederhana dibanding menjumlah peluang 0 hingga 7.
b(8;10;0,6) = 0,121
b(9;10;0,6) = 0,040
b(10;10;0,6) = 0,006
= 0,167 dengan demikian peluang x < 7 = 1 - 0,167 = 0,833
2. Distribusi Poison
Berbeda dengan distribusi binomial, distribusi poisson memiliki ciri-ciri :
a. peluang terjadinya suatu kejadian sangat jarang atau sangat sering (mendekati 0 atau mendekati 1);
b. nilai rata-rata bisa diketahui dengan cara 𝞵 = n.p ;\
c. n lebih dari atau sama dengan 30
Rumus poison :
𝞵 = rata-rata populasi
x = nilai yang diharapkan
e = nilai eksponensial = 2,71828 (berlaku tetap)
p = jumlah peluang
Kita coba saja langsung menggunakan contoh kasus berikut :
Apabila diketahui probabilitas seseorang akan meninggal karena terkena penyakit anjing gila adalah 0,01. Sementara itu, rata-rata orang yang meninggal akibat menderita penyakit anjing gila adalah 2 orang.
Hitunglah peluang untuk :
a. 3 orang akan meninggal !
b. tidak lebih dari 1 orang yang meninggal !
c. lebih dari 2 orang meninggal !
Untuk soal nomor satu, kita gunakan perhitungan dengan menggunakan rumus dan juga tabel distribusi poison, sedangkan untuk soal dua dan tiga kita hanya gunakan tabel distribusi poison.
Penggunaan tabel juga seperti halnya binomial, kita harus perhatikan apakah tabel tersebut kumulatif atau tidak. Dalam BMP ini, yang kita gunakan adalah tabel yang tuidak kumulatif.
Jawaban Kasus :
b. Yang dicari adalah tidak lebih dari 1 orang yang meninggal sehingga kemungkinannya kalau tidak 1 orang yang meninggal atau tidak ada sama sekali yang meninggal (0).
Dengan kata lain x < 1. Untuk menggunakan tabel maka kita hanya perlu melihat nilai x dan nilai rata-ratanya.
Kita lihat cuplikan tabel berikut : (tabel lengkapnya bisa anda lihat dalam lampiran tabel)


c. Nilai x (peluang yang dicari) adalah lebih dari 2 orang meninggal sehingga x > 2 maka kita harus mencari akumulasi dari peluang untuk 0, peluang untuk 1, dan peluang untuk 2. Setelah hasilnya kita dapatkan maka kita tinggal mengurangi 1 dengan hasil tersebut karena sebenarnya yang akan kita cari adalah nilai yang lebih dari 2.
P(2,0) = 0,13534
P(2,1) = 0,27067
P(2,2) = 0,27067
= 0,67668 dengan demikian peluang x > 2 = 1 - 0,67668 = 0,32332
B. DISTRIBUSI PROBABILITA KONTINU
Seperti namanya, distribusi kontinu pun digunakan pada variabel kontinu untuk melihat peluang dari beberapa kejadian yang memiliki nilai pecahan.
Beberapa distribusi yang memiliki ciri kontinu adalah distribusi normal, distribusi normal pada binomial, distribusi t-student, distribusi x² (chi-square), dan distribusi F. Dalam modul ini, yang akan kita pelajari hanya distribusi normal dan distribusi normal pada binomial karena kedua distribusi inilah yang sering digunakan dalam ilmu sosial.
1. Distribusi Normal
Distribusi normal memiliki karakteristik sebagai berikut :
a. Bentuk kurva seperti lonceng.
b. Nilai rata-rata sampel, median, serta modus berada di titik tengah data.
c. Dua sisi kurva tidak pernah menyentuh garis horizontal.
d. Total peluang di bawah kurva = 1 (100%). Karena bentuknya simetris, maka luas area dari titik tengah ke kiri atau dari titik tengah ke kanan sama dengan 0,5
e. 68,26% dari data terletak pada 1 (standard deviasi)
Distribusi normal dipengaruhi oleh besar kecilnya simpangan baku.
Pada distribusi normal, kurva yang memiliki simpangan baku yang lebih kecil, akan memiliki bentuk kurva yang lebih runcing, dengan demikian data akan lebih terpuasat, sedangkan apabila simpangan baku besar maka data akan lebih menyebar. Dengan demikian, semakin kecil simpangan baku maka kecendrungan data akan semakin baik.
Untuk kurva dengan rata-rata berbeda maka bentuk kurva akan sama, namun lokasi pemusatannya berbeda.
Untuk menghitung distribusi normal, kita bisa memakai rumus berikut :
Rumus : Z = x - 𝞵
𝞼
Contoh :
Apabila seorang pekerja bisa menghasilkan batu bata rata-rata sebanyak 500/hari, dengan deviasi : 100/hari maka berapa peluang seorang pekerja dapat menghasilkan batu bata sebanyak 500-650 dalam satu hari?
Jawab :
Langkah pertama; kita hitung nilai untuk 650 berdasar rumus
Z = (650-500)/100 = 1,5. Setelah kita sudah mendapat angka hasil perhitungan, kita bisa lihat pada tabel cuplikan normal nilai untuk 1,5 adalah 0,4332 (tabel lengkap bisa dilihat di bagian lampiran).
Langkah kedua; kita hitung nilai untuk 500 dengan memakai rumus Z = (500 - 5600) / 100 = 0. Setelah kita telah mendapat angka hasil perhitungan, kita bisa lihat pada cuplikan tabel normal nilai untuk 0 adalah 0,0000 (tabel lengkap bisa dilihat di bagian lampiran).
Langkah ketiga; kita kurangi hasil yang ditunjukkan oleh tabel tadi, yaitu 0,4332 - 0 = 0,4332, mengapa kita harus melakukan tiga tahap ini? Apabila kita perhatikan kurva berikut maka kita akan tahu bahwa kita dapat menghitung peluang seseorang bila ia menyelesaikan batu bata sebanyak 500 sehari.
Kita juga dapat menghitung peluang seseorang untuk menyelesaikan batu bata sebanyak 650 sehari. Sementara itu, yang kita cari adalah peluang orang tersebut menyelesaikan batu bata sebanyak 500 hingga 650. Dengan demikian, kita bisa tahu berapa peluangnya dengan mengurangi peluang untuk 650 dengan peluang untuk 500. Untuk lebih jelasnya, kita bisa perhatikan kurva yang menggambarkan luas area yang kita cari dalam kurva berikut :
Dengan demikian, peluang seseorang untuk membuat batu bata 500 hingga 650 dalam sehari adalah 0,4332
Saudara Mahasiswa, anda telah mempelajari mengenai distribusi probabilita normal, Kini cobalah kerjakan tugas berikut ini, untuk membantu anda memahami materi yang telah anda pelajari. Cobalah mengerjakan sendiri, kemudian cocokkan denganjawaban yang ada di bawah tugas ini.
Diketahui nilai rata-rata ujian pengantar statistik sosial adalah 50 dengan standar deviasi 10. Tentukanlah peluang nilai yang dicapai mahasiswa yang berada :
- kurang dari 40
- antara 45 - 50
- lebih dari 60
Jawaban untuk ksus pertama :
0,3413 adalah luas area dari 40 ke 50. Karena luas area dari sisi paling kiri (0) ke sisi tengah (50) adalah 0,5. sedangkan yang akan kita cari hanya dari 0 ke 40 maka kita harus mengurangi 0,5 dengan 0,3414 sehingga peluang nilai mahasiswa kurang dari 40 adalah 0,1587
Jawaban untuk kasus kedua :
Jawaban untuk kasus ketiga :
Seperti halnya pada kasus pertama, 0,3413 adalah luas area dari 50 ke 60. Karena luas area dari sisi paling kanan ke sisi tengah (50) adalah 0,5, sedangkan yang akan kita cari hanya dari 60 dan seterusnya maka kita harus mengurangi 0,5 dengan 0,3413 sehingga peluang nilai mahasiswa lebih dari 60 adalah 0,1587
2. Distribusi Normal pada Binomial
Distribusi normal pada binomial terjadi ketika suatu kejadian memiliki ciri-ciri normal dan juga binomial. Misalnya, kita memiliki data yang jumlahnya lebih dari 30, tetapi memiliki ciri-ciri binomial, apa yang harus dilakukan? Kita dapat menggunakan distribusi normal pada binomial.
Distribusi inbi mempunyai ciri-ciri :
a. varibaelnya memilki 2 kategori;
b. n > 30;
c. p = 0,5;
d. memiliki nilai koreksi kontinuitas. Prinsip koreksi kontinuitas adalah memperluas area yang dicari;
e. rata-rata bisa dicari dengan menggunakan rumus 𝞵 = np ;
f. simpangan baku bisa dicari dengan menggunakan rumus 𝜎 = ⎷ npq ;
g. rumus yang digunakan adalah rumus distribusi normal
Rumus : Z = x - 𝞵
𝞼
Kita langsung saja dengan menggunakan contoh berikut :Peluang seorang pekerja menghasilkan produk 50 dalam satu jam adalah 0,46. Jika dipilih 32 pekerja secara acak maka hitunglah peluang :
- 20 pekerja mampu menghasilkan 50 produk dalam satu jam, dan
- antara 13 - 16 pekerja mampu menghasilkan 50 produk dalam satu jam
Jawaban kasus pertama :
Dengan menggunakan koreksi kontinuitas maka are harus diperluas. Karena yang dicari adalah titik (dalam kasus ini 20) maka nilai x diperluas 0,5 ke kiri dan ke kanan sehingga nilai x yang dicari menjadi 19,5 sampai 20,5.
Jawaban kasus kedua :
X = antara 13 sampai 16
Dengan menggunakan koreksi kontinuitas maka area harus diperluas 0,5 ke kiri dan ke kanan sehingga nilai x yang dicari menjadi 12,5 sampai 16,5.
MODUL 5
PENARIKAN SAMPEL
Dalam penelitian yang dilakukan di lingkungan ilmu sosial, sering kali tidak memungkinkan untuk meneliti terhadap seluruh populasi yang ada. Bayangkan saja, jika kita ingin mengetahui bagaimana harapan warga masyarakat Indonesia terhadap presiden terpilih. Jumlah warga Indonesia lebih dari 300 juta jiwa. Tentunya sulit bagi kita untuk melakukan penelitian tersebut. Pertanyaan yang kemudian muncul adalah apakah kita pada akhirnya tidak jadi melakukan penelitian tersebut? Tentunya bukan itu akhirnya. Kita bisa menyiasati persoalan yang terjadi itu dengan melakukan cara yang disebut dengan mengambil sampel.
Apa pengertian dari sampel? Bagaimana kita bisa mengambil sampel? Kedua hal inilah yang mendasari kita untuk mempelajari Modul 5 ini. Modul ini, akan membahas mengenai apa itu sampel, bagaimana cara kita menarik sampel, dan tentunya materi ini harus didahului dengan mempelajari apa itu populasi.
Populasi adalah keseluruhan elemen yang akan kita teliti. Dalam contoh kasus yang kita sebut tadi, populasi penelitiannya adalah seluruh warga negara Indonesia. Sering kali kita membatasi populasi kita ke dalam cakupan yang lebih sempit. Dengan kata lain, populasi setidaknya mencakup 3 unsur, yaitu isi, cakupan, dan waktu.
Dengan adanya ketiga unsur ini maka kita bisa lebih memastikan kebenaran dari populasi. Kembali ke contoh yang ada maka isinya adalah seluruh warga negara Indonesia, cakupannya yang berusia 17 tahun ke atas, dan waktunya adalah pada tahun 2015. Dengan demikian, mobil ini sangat berguna bagi Anda yang bekerja di lingkup penelitian.
Unsur yang tercakup dalam populasi ada tiga unsur; yaitu isi, cakupan, dan waktu. Kita coba ambil contoh lain, agar anda menjadi lebih jelas dalam penelitian sikap pelajar SLTA yang akan berimigrasi ke kota. maka populasinya adalah seluruh pelajar SLTA yang tinggal di desa Ora Wani pada tahun 2015.
Isi : pelajarSLTA
Cakupan : tinggal di desa Ora Wani
Waktu : tahun 2015